NCERT Exemplar Class 7 Maths Book PDF Download Chapter 10 Algebraic Expression Solutions
Multiple Choice Questions (MCQs)
Question 1:
An algebraic expression containing three terms is called a
(a) monomial
(b) binomial
(c) trinomial
(d) All of these
Solution:
(c) An algebraic expression containing one term is called monomial, two terms is called binomial and three terms is called trinomial.
Question 2:
Number of terms in the expression 3x2y -2y2z-z2x+ 5 is
(a) 2 (b) 3 (c) 4 (d) 5
Solution:
(c) The terms in the expression are 3x2y, -2y2z, -z2x and 5. Hence, total number of terms are 4.
Question 3:
The terms of expression 4x2 -3xy are
(a) 4x2 and -3xy
(b) 4x2 and 3xy
(c) 4x2 and -xy
(d) x2 and xy
Solution:
(a) Terms in the expression 4x2 -3xy are 4x2 and -3xy.
Question 4:
Factors of -5x2y2z are
(a) -5 x x x y x z
(b) -5 x x2 x y x z
(c) -5 x x x x x y x y x z
(d) -5 x x x y x z2
Solution:
(c) -5x2y2z can be written as -5 x x x x x y x y x z.
Question 5:
Coefficient of x in -9xy2z is
(a) 9 yz
(b) -9 yz
(c) 9 y2z
(d) -9 y2z
Solution:
(d) Coefficient of x in-9x2yz = – 9y2z
Question 6:
Which of the following is a pair of like terms?
(a) -7xy2z, -7x2yz
(b) -10xyz2, 3xyz2
(c) 3xyz, 3x2y2z2
(d) 4xyz2, 4x2yz
Solution:
(b) Like terms are those terms, having same algebraic factor.
Hence, -10ayz2 and 3ayz2 are like terms as they contain xyz2 same factor.
Question 7:
Identify the binomial out of the following
(a) 3xy2 + 5y – x2y
(b) x2y-5y-x2y
(c) xy + yz + zx
(d) 3xy2 + 5y-xy2
Solution:
(d) We know that, an algebraic expression containing two terms is called binomial. So, taking option (d), 3xy2 + 5y-xy2 = 2x2y + 5y As it contains only two terms, hence it is known as binomial.
Question 8:
The sum of x4 – xy+2y2 and -x4 + xy+2y2 is
(a) monomial and polynomial in y
(b) binomial and polynomial
(c) trinomial and polynomial
(d) monomial and polynomial in x
Solution:
(a) Required sum = (x4-xy+2y2)+ (-x4 + xy+2y2)
= x4-xy+2y2-x4+ xy+2y2 = [(x4 + (-x4)] + (-xy+xy)+(2y2 + 2y2)
= 0+ 0+ 4y2 = 4y2
4y2 is a monomial and polynomial in y.
Question 9:
The subtraction of 5 times of y from x is
(a) 5x-y
(b) y-5x
(c) x-5y
(d) 5y-x
Solution:
(c) 5 times of y = 5y
Now, subtraction of 5 times of y from x is written as x-5y.
Question 10:
-b- 0 is equal to
(a) -1 x b (b) 1-b-0 (c) 0-(-1) x b (d) -b—0 —1
Solution:
(a) We have, -b-0=-b
(a)-1 x b=-b
(b) 1-b-0=1-b
(c) 0-(-1) x b=0+b=b
(d) -b-0-1=-b-1
Hence, option (a) is correct.
Question 11:
The side length of the top of square table is x. The expression for perimeter is
(a) 4 + x (b) 2x (c) 4x (d) 8x
Solution:
(c) Given, side length of a square table = x
∴Perimeter of a square = 4x
Side = 4 x x =4x.
Question 12:
The number of scarfs of length half metre that can be made from y metres of cloth is
(a) 2y (b) y/2 (c) y + 2 (d) y + ½
Solution:
(a) We have,
Length of 1 scarf =½ m
So, number of scarfs which can be made from y metres =y/(½)=2 y.
Question 13:
123x2y-138x2y is a like term of
(a) 10xy (b) -15xy (c)-15xy2 (d) 10x2y
Solution:
(d) We have, 123x2y-138x2y=-15x2y
Hence, it is like term of 10x2y as both contain x2y.
Question 14:
The value of 3x2 – 5x + 3, when x=1 is
(a) 1 (b) 0 (c)-1 (d)11
Solution:
(a) Putting x=1 in given equation we get 3x2-5x + 3= 3(1)2-5(1)+3 =3-5+3 =1
Question 15:
The expression for the number of diagonals that we can make from one vertex of a n-sided polygon is
(a) 2n +1 (b) n -2 (c) 5n + 2 (d)n-3
Solution:
(d) Since, vertex is formed by joining two sides. Diagonal is line segment joining the two opposite vertex. So, number of diagonal formed by one vertex =n-3.
Question 16:
The length of a side of square is given as 2x+3. Which expression represents the perimeter of the square?
(a) 2x +16 (b) 6x + 9 (c) 8x + 3 (d) 8x + 12
Solution:
(d) Given, side of the square = (2x + 3)
∴ Perimeter of square = 4 x (Side)
= 4 x (2x + 3)
= 8x + 12
Fill in the Blanks
In questions 17 to 32, fill in the blanks to make the statements true.
Question 17:
Sum or difference of two like terms is ………………..
Solution:
Sum or difference of two like terms is a like term, e.g. 138x2y-125x2y = 13x2y
Question 18:
In the formula, area of circle =πr2, the numerical constant of the expression πr2 is …………….
Solution:
In πr2, the numerical constant is π as r2 is variable.
Question 19:
3a2b and -7ba2 are ………………… terms.
Solution:
3a2b and -7ba2 are like terms as both have same algebraic factor a2b.
Question 20:
-5a2b and -5b2a are ……………. terms.
Solution:
-5a2b and -5b2a are unlike terms as they do not have same algebraic factor.
Question 21:
In the expression 2πr, the algebraic variable is …………….
Solution:
In the expression 2πr,2π is constant while r is an algebraic variable.
Question 22:
Number of terms in a monomial is …………….
Solution:
Number of terms in a monomial is one.
Question 23:
Like terms in the expression n(n+1)+6(n-1) are …………….. and ……………….
Solution:
We have, n(n+1)+ 6(n – 1)=n2 + n+6n-6
Hence, like terms in the expression n(n+1)+6(n-1)are n and 6n.
Question 24:
The expression 13+90 is a ……………….
Solution:
∴ 13+ 90=103
∴ 103 is a constant term.
Question 25:
The speed of car is 55 km/h. The distance covered in y hours is ………………
Solution:
Given, speed of car = 55 km/h.
∴ Distance = Speed x Time
∴Distance covered in y hours = 55xy = 55y km
Question 26:
x+y+z is an expression which is neither monomial nor …………..
Solution:
Since, x+ y+z has three terms, so it is trinomial.
Hence, x + y+z is an expression which is neither monomial nor binomial.
Question 27:
If (x2y+y2 + 3) is subtracted from (3x2y+2y2 + 5), then coefficient of y in the result is ……………….
Solution:
We have, (3x2y+2y2 + 5)-(x2y+ y2 + 3) = 3x2y+2y2 + 5-x2y-y2-3
= 2x2y+y2+2
Coefficient of y = 2x2
Question 28:
-a-b-c is same as -a- (…………….).
Solution:
We have, -a-b-c=-a-(b+c) [by taking common (-) minus sign]
So,-a-b-c is same as -a-(b+ c).
Question 29:
The unlike terms in perimeters of following figures are …………….. and ……………….

Solution:
In Fig. (i),
Perimeter = Sum of all sides
= 2x + y+2x + y = 4x + 2y
In Fig. (ii),
Perimeter = Sum of all sides
= x+ y2 + x+ y2=2x + 2y2
Unlike terms in perimeters are 2y and 2y2.
Question 30:
On adding a monomial ……………… to -2x+4y2+z, the resulting expression becomes a binomial.
Solution:
We can add 2x, -4y2 and -z to the expression to make it binomial.
=> 2x + (-2x + 4y2 + z) = 4y2 + z
=> -4y2 + (-2x + 4y2 + z) = -2x + z
=> -z + (-2x + 4y2 + z) = -2x + 4y2
Hence, on adding a monomial 2x or -4y2 or -z to -2x + 4y2 + z, the resulting expression becomes a binomial.
Question 31:
3x+23x2 + 6y2 + 2x+y2 + ………….. =5x+7y2.
Solution:
Let(3x+23x2 + 6y2+2x+y2)+ M = 5x + 7y2
=> M=(5x+7y2)-(3x + 23x2 + 6y2+2x+ y2)
=> M = 5x + 7y2-3x- 23x2– 6y2 -2x – y2
[with -ve sign, +ve sign in the bracket will change on opening it]
=> M = 5x-3x-2x + 7y2-6y2-y2-23x2
M = 0 + 0 – 23x2 =-23x2
Question 32:
If Rohit has 5xy toffees and Shantanu has 20yx toffees, then Shantanu has ………… more toffees.
Solution:
We have, Rohit has toffees =5xy
Shantanu has toffees =20yx
Difference = 20xy -5xy=15xy
Hence, Shantanu had 15xy more toffees.
True/False
In questions 33 to 52, state whether the statements given are True or False.
Question 33:
1+(x/2)+x3 is a polynomial.
Solution:
True
Expression with one or more than one term is called a polynomial.
Question 34:
(3a-b+3)-(a+b) is a binomial.
Solution:
False
We have , (3a-b+3)-(a + b)= 3a-b+3-a-b
= 3a-a-b-b + 3 = 2a-2b+ 3
The expression has three terms, it is a trinomial.
Question 35:
A trinomial can be a polynomial.
Solution:
True
Trinomial is a polynomial, because it has three terms.
Question 36:
A polynomial with more than two terms is a trinomial.
Solution:
False
A polynomial with more than two terms can be trinomial or more. While a trinomial have exact three terms.
Question 37:
Sum of x andy is x+y.
Solution:
True
Sum of x and y is x+y.
Question 38:
Sum of 2 and p is 2p.
Solution:
False
Sum of 2 and p is 2 + p.
Question 39:
A binomial has more than two terms.
Solution:
False
Binomial has exactly two unlike terms.
Question 40:
A trinomial has exactly three terms.
Solution:
True
A trinomial has exactly three unlike terms.
Question 41:
In like terms, variables and their powers are the same.
Solution:
True
In like terms, algebraic factors are same.
Question 42:
The expression x+y+5x is a trinomial.
Solution:
False
∴ x+ y + 5x =6x+ y It is a binomial.
Question 43:
4p is the numerical coefficient of q2 in -4pq2.
Solution:
False
Numerical coefficient of q2 in -4pq2 =-4.
Question 44:
5a and 5b are unlike terms.
Solution:
True
Because both the terms have different algebraic factors.
Question 45:
Sum of x2 + x and y+y2 is 2x2 + 2y2.
Solution:
False
∴ Sum = (x2 + x) + (y+ y2) = x2 + x + y + y2 = x2 + y2 + x+y
Question 46:
Subtracting a term from a given expression is the same as adding its additive inverse to given expression.
Solution:
True
Because additive inverse is the negation of a number or expression.
Question 47:
The total number of planets of Sun can be denoted by the variable n.
Solution:
False
As, Sun has infinite planets around it.
Question 48:
In like terms, the numerical coefficients should also be the same.
Solution:
False
e.g. -3x2y and 4x2y are like terms as they have same algebraic factor x2y but have different numerical coefficients.
Question 49:
If we add a monomial and binomial, then answer can never be a monomial.
Solution:
False
If we add a monomial and a binomial, then answer can be a monomial, e.g. Add x2 and -x2 + y2
= x2 + (-x2 + y2)
= x2 – x2 + y2 = y2
Hence, the answer is monomial.
Question 50:
If we subtract a monomial from a binomial, then answer is atleast a binomial.
Solution:
False
If we subtract a monomial from a binomial, then answer is atleast a monomial, e.g. Subtract x and x-y= x-(x-y) = x-x + y = y, i.e. monomial.
Hence, the answer is monomial.
Question 51:
When we subtract a monomial from trinomial, then answer can be a polynomial.
Solution:
True
When we subtract a monomial from a trinomial, then answer can be binomial or polynomial.
e.g. Subtract y2 from y2 -x2 -2xy.
= (y2 -x2 – 2xy)-y3 = y2 – y2 -x2 -2xy = -x2 – 2xy Hence, answer is binomial.
Question 52:
When we add a monomial and a trinomial, then answer can be a monomial.
Solution:
False
When we add a monomial and a trinomial, then it can be binomial or trinomial, e.g. Add xy and x3 + 2xy-y3
= xy+ (x3 +2 xy-y3)
= xy+2xy+ x3 – y3 = 3xy + x3 – y3 Hence, answer is trinomial.
Question 53:
Write the following statements in the form of algebraic expressions and write whether is monomial, binomial or trinomial.
(a) x is multiplied by itself and then added to the product of x and y.
(b) Three times of p and two times of q are multiplied and then subtracted from r.
(c) Product of p, twice of q and thrice of r.
(d) Sum of the products of a and b, b and c, c and a.
(e) Perimeter of an equilateral triangle of side x.
(f) Perimeter of a rectangle with length p and breadth q.
(g) Area of a triangle with base m and height n.
(h) Area of a square with side x.
(i) Cube of s subtracted from cube of t.
(j) Quotient of x and 15 multiplied by x.
(k)The sum of square of x and cube of z.
(l) Two times q subtracted from cube of q.
Solution:

Question 54:
Write the coefficient of x2 in the following:

Solution:

Question 55:
Find the numerical coefficient of each of the terms

Solution:

Question 56:
Simplify the following by combining the like terms and then write
whether the expression is a monomial, a binomial or a trinomial.

Solution:

Question 57:
Add the following expressions
(a) p2-7pq-q2 and -3p2 -2pq+7q2
(b) x3 -x2y-xy2 -y3 and x3 -2x2y+3xy2 +4y
(c) ab + bc+ca and -bc-ca-ab
(d) p2 -q + r ,q2 -r+p and r2-p+q
(e) x3y2 +x2y3 +3y4 and x4 +3x2y3 +4y4
(f) p2qr+pq2r+pqr2 and -3pq2r-2pqr2
(g) uv-vw, vw-wu and wu-uv
(h) a2 +3ab-bc, bz +3bc-ca and c2 +3ca-ab

Solution:



Question 58:
Subtract
(a) -7p2qr from -3p2qr.
(b) -a2 -ab from b2 +ab.
(c) -4x2y-y3 from x3 +3xy2 -x2y.
(d) x4 +3x3y3 +5y4 from 2x4 -x3y3 +7y4.
(e) ab-bc- ca from -ab+bc+ ca.
(f) -2a2-2b2 from -a2 -b2 +2ab.
(g) x3y3 +3x2y2 -7xy3 from x4 +y4 +3x2y2 -xy3.
(h) 2(ab+bc+ca) from -ab-bc-ca.
(i) 4.5x5 -3.4x2 +5.7 from 5x4 -3.2x2 -7.3x.
(j) 11-15y2 from y3 -15y2 -y-11.
Solution:


Question 59:
(a) What should be added to x3 +3x2y + 3xy2 +y3 to get x3 +y3?
(b) What should be added to 3pq+5p2q2 +p3 to get p3 +2p2q2 +4pq ?
Solution:

Question 60:
(a) What should be subtracted from 2x3 -3x2y+2xyz +3y3 to get x3 -2x2y+3xy2 +4y3?
(b) What should be subtracted from -7mn+2m2 +3n2 to get m2 +2mn+n2?
Solution:

Question 61:
How much is 21a3 -17a2 less than 89a3 -64a2+6a+16 ?
Solution:
Required expression is
89a3 -64a2+6a+16-(21a3 -17a2)
=89a3 -64a2+6a+16 -21a3 + 17a2 On combining the like terms,
= 89a3 -21a3 – 64a2 +17a2 + 6a+16 = 68a3 -47a2 + 6a+16
So,21a3 -17a2 is 68a3-47a2 + 6a+16 less than 89a3 -64a2+6a+16.
Question 62:
How much is y4 -12y2 +y+14 greater than 17y3+34y2 -51y+68?
Solution:
Required expression is
y4 -12y2 +y+14-(17y3+34y2 -51y+68)
=y4 -12y2 +y+14-17y3-34y2 +51y-68 On combining the like terms,
=y4-12y2-34y2 + y+51y+14-68-17y3 = y4-46y2 + 52y-17y3 -54 =y4 -17y3 -46y2 + 52y-54
So, y4 -12y2 +y+14 is y4-17y3-46y2 + 52y-54 greater than 17y3+34y2 -51y+68.
Question 63:
How much does 93p2 -55p+4 exceed 13p3 -5p2 + 17p-90?
Solution:
Required expression is
93p2 -55p+4 —(13p3 -5p2 + 17p-90)
= 93p2 -55p+4 -13p3+5p2 – 17p + 90
On combining the like terms,
= 93p2 + 5p2-55p-17p+4+90-13p3 = 98p2-72p+94-13p3 =-13p3 + 98p2-72p+ 94
So, 93p2 -55p+4 is -13p3 + 9p2 -72p+ 94 exceed from 13p3 -5p2 + 17p-90.
Question 64:
To what expression must 99x3 -33x2 -13x-41 be added to make the sum zero?
Solution:
In order to find the solution, we will subtract 99x3 -33x2 -13x-41 from 0.
Required expression is
0- (99x3 -33x2 -13x-41) = 0- 99x3 +33x2 +13x+41
= – 99x3 +33x2 +13x+41
So, If we add -99x3 +33x2 +13x+41 to 99x3 -33x2 -13x-41, then the sum is zero.
Question 65:
Subtract 9a2 – 15a +3 from unity.
(a) a2 +2ab+b2
(b) a2-2ab+b2
(c) a3 +3a2b+3ab2 + b3
(d) a3 -3a2b+3ab2 -b3
(e) (a2+b2)/3
(f) (a2 – b2)/3
(g) (a/b) + (b/a)
(h) a2 +b2 -ab-b2 -a2
Solution:
In order to find solution, we will subtract 9a2 -15a + 3 from unity, i.e. 1. Required’expression is
1- (9a2-15a+3)=1- 9a2 + 15a – 3
=-9a2+15a-2
Question 66:
Find the values of the following polynomials at a = -2 and b=3.

Solution:

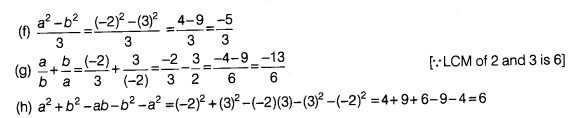
Question 67:
Find the values of following polynomials at m = 1, n = -1 and p=2
(a) m+n+p
(b) m2+n2+P2
(c) m3+ n3+p3
(d) mn+np + pm
(e) m3 +n3 + p3 -3mnp
(f) m2n2 +n2p2 +p2m2
Solution:
Given, m=1, n=-1 and p=2
So, putting m = 1, n = -1 and p = 2 in the given expressions, we get
(a) m+n+p=1-1+2=2
(b) m2+n2+P2 =(1)2 + (-1)2 + (2)2 =1+1+ 4=6
(c) m3+ n3+p3 =(1)3 + (-1)3 + (2)3 =1 -1 + 8 = 8
(d) mn+np+ pm=(1)(-1)+(-1)(2)+(2)(1)=-1-2 + 2 =-1
(e) m3 +n3 + p3 -3mnp =(1)3 + (-1)3 + (2)3 -3(1)(-1)(2) =1-1+8+6=14
(f) m2n2 +n2p2 +p2m2 =(1)2 (-1)2 + (-1)2 (2)2 + (2)2 (1)2 =1+ 4+ 4=9
Question 68:
If A=3x2 -4x+1, B=5x2+3x-8 and C=4x2 -7x+3, then find
- (A + B)-C
- B+C-A
- A-B+C
Solution:
Given, A = 3x2 – 4x +1, B = 5x2 + 3x – 8 and C = 4x2 – 7x + 3
- (A + B)-C =(3x2 -4x +1 + 5x2 + 3x-8) -(4x2 -1x + 3)
On combining the like terms,
= (3x2 + 5x2 – 4x + 3x + 1 – 8) – (4x2 – 1x + 3) =(8x2-x-7)-(4x2-7x + 3)
= 8x2-x-7-4x2 + 7x-3 = 8x2-4x2 -x + 7x-7-3 =4x2 + 6x-10 - B+C-A
= 5x2 + 3x-8+4x2-7x + 3-(3x2-4x + 1))
On combining the like terms,
= (5x2 + 4x2 + 3x-7x-8+ 3)-(3x2 – 4x + 1)
= (9x2 -4x-5)- (3x2 – 4x +1)
= 9x2 -4x-5-3x2 + 4x-1 = 9x2 – 3x2 – 4x + 4x – 5 -1 = 6x2-6 - A+B+C
= 3x2-4x+ 1 +5x2 + 3x-8+4x2-7x+3 On combining the like terms,
= 3x2 + 5x2 + 4x2 -4x + 3x-7x +1 – 8 + 3 = 12x2-8x-4
Question 69:
If P = -(x-2), Q = -2(y+1) and R=- x+2y, find a,when P+Q+ R=ax.
Solution:
Given, P = -(x-2),Q = -2(y+ 1)and R = -x + 2y Also given, P+Q + R=ax
On putting the values of P,Q and R on LHS, we get -(x-2)+[-2(y+1)]+(-x+2y) = ax => -x+2 + (-2y-2)-x + 2y = ax
=> -x + 2 – 2y – 2 – x+ 2y = ax
On combining the like terms,
-x – x – 2y + 2y + 2 – 2=ax => -2x = ax
By comparing LHS and RHS, we get a = -2
Question 70:
From the sum of x2 – y2 – 1, y2 – x2 – 1 and 1 – x2 – y2, subtract -(1 + y2).
Solution:
Sum of x2 – y2 -1, y2 – x2 – 1 and 1 – x2 – y2 = x2 – y2 – 1 + y2 – x2 – 1 + 1 – x2 – y2 On combining the like terms,
= x2 – x2 – x2 – y2 + y2 – y2 – 1 – 1 + 1 = -x2 – y2 – 1
Now, subtract -(1 + y2) from -x2 – y2 -1
= -x2 – y2 -1 – [-(1 + y2)]
= – x2 – y2 – 1 + 1 + y2 = -x2 – y2 + y2 – 1 + 1 = -x2
Question 71:
Subtract the sum of 12ab – 10b2 – 18a2 and 9ob + 12b2 + 14a2 from the sum of ab + 2b2 and 3b2 – a2.
Solution:
Sum of 12ab-10b2 -18a2 and 9ab + 12b2 + 14a2 = 12ab – 10b2 – 18a2 + 9ab + 12b2 + 14a2
On combining the like terms,
= 12ab + 9ab – 10b2 + 12b2 – 18a2 + 14a2 = 21 ab +2b2 – 4a2
Sum of ab + 2b2 and 3b2 – a2 = ab + 2b2 + 3b2 – a2 = ab + 5b2 – a2
Now, subtracting 21ab + 2b2 – 4a2 from ab + 5b2 – a2, we get = (ab + 5b2 – a2) – (21ab + 2b2 – 4a2)
= ab+ 5b2 – a2 – 21ab – 2b2 + 4a2 On combining the like terms,
= ab – 21ab + 5b2 – 2b2 – a2 + 4a2 = – 20ab + 3b2 + 3a2 = 3a2 + 3b2 – 20ab
Question 72:
Each symbol given below represents an algebraic expression.

Find the expression which is represented by the above symbols.
Solution:

Question 73:
Observe the following nutritional chart carefully

Write an algebraic expression for the amount of carbohydrates (in grams) for
(a) y units of potatoes and 2 units of rajma.
(b) 2x units tomatoes and y units apples.
Solution:
(a) By unitary method,
∴ 1 unit of potatoes contain carbohydrates = 22 g
y units of potatoes contain carbohydrates =22 x y = 22y g
Similarly,
∴ 1 unit of rajma contain carbohydrates = 60 g
∴ 2 units of rajma contain carbohydrates =(60 x 2) = 120 g
Hence, the required expression is 22 y +120.
(b) By unitary method,
∴ 1 unit of tomatoes contain carbohydrates = 4 g
∴ 2x units of tomatoes contain carbohydrates = 2x x 4= 8x g
Similarly,
∴ 1 unit apples contain carbohydrates = 14 g y units apples contain carbohydrates = 14 x y = 14y g Hence, the required expression is 8x +14y.
Question 74:
Arjun bought a rectangular plot with length x and breadth y and then sold a triangular part of it whose base is y and height is z. Find the area of the remaining part of the plot.
Solution:

Question 75:
Amisha has a square plot of side m and another triangular plot with base and height each to m. What is the total area of both plots?
Solution:

Question 76:
A taxi Service charges Rs. 8 per km levies a fixed charge of Rs. 50. Write an algebraic expression for the above situation, if the taxi is hired for x km.
Solution:
As per the given information, taxi service charges Rs. 8 per km and fixed charge of ? 50.
If taxi is hired for x km.
Then, algebraic expression for the situation = 8 x x + 50 = 8x + 50 Hence, the required expression is 8x + 50.
Question 77:
Shiv works in a mall and gets paid Rs. 50 per hour. Last week he worked for 7 h and this week he will work for x hours. Write an algebraic expression for the money paid to him for both the weeks.
Solution:
Given, money paid to shiv = Rs. 50 per h.
∴ Money paid last week =Rs. 50 x 7 = Rs. 350
So, money paid this week = Rs. 50 x x = Rs. 50x
Total money paid to shiv =Rs. (350 + 50x) =Rs. 50(x + 7)
Question 78:
Sonu and Raj have to collect different kinds of leaves for science project. They go to a park where Sonu collects 12 leaves and Raj collects x leaves. After some time Sonu loses 3 leaves and Raj collects 2x leaves. Write an algebraic expression to find the total number of leaves collected by both of them.
Solution:
According to the question,
Sonu collected leaves = 12-3=9
Raj collected leaves =x + 2x=3x
∴ Total leaves collected =9 + 3x
Hence, the required expression is 9+ 3x.
Question 79:
A school has a rectangular playground with Length x and breadth y and a square lawn with side x as shown in the figure given below. What is the total perimeter of both of them combined together?

Solution:

Question 80:
The rate of planting the grass is Rs. x per square metre. Find the cost of planting the grass on a triangular lawn whose base is y metres and height is z metres.
Solution:

Question 81:
Find the perimeter of the figure given below.

Solution:
We know that, perimeter is the sum of all sides.
Perimeter of the given figure = AB + BC + CD + DA
=(5x – y)+2 (x + y)+ (5x – y)+2(x + y) = 5x – y + 2x + 2y + 5x – y + 2x + 2y
On combining the like terms,
= 5x + 2x+ 5x + 2x – y + 2y – y + 2y =14x + 2y
Question 82:
In a rectangular plot, 5 square flower beds of side (x+2) metres each have been laid (see the figure). Find the total cost of fencing the flower beds at the cost of Rs. 50 per 100 metres.

Solution:

Question 83:
A wire is (7x-3) metres long. A length of (3x—4) metres is cut for use, answer the following questions
(a) How much wire is left?
(b) If this left out wire is used for making an equilateral triangle. What is the length of each side of the triangle so formed?
Solution:
Given, length of wire = (7x – 3)m
and wire cut for use has length = (3x – 4) m
(a) Left wire=(7x – 3) – (3x – 4)=7x – 3 – 3x + 4=7x – 3x – 3 + 4 =(4x + 1)m
(b) ∴ Left wire = (4x +1)m
∴ Perimeter of equilateral triangle = Length of wire left
=> 3 x (side) = 4x + 1
=> side = (4x +1)/3 = 1/3 (4x + 1)m.
Question 84:
Rohan’s mother gave him Rs. 3xy2 and his father gave him Rs. 5(xy2 + 2). Out of this money he spent Rs. (10 – 3xy2) on his birthday party. How much money is left with him?
Solution:
Given, amount given to Rohan by his mother =Rs. 3xy2 and amount given to Rohan by his father =Rs. 5(xy2 + 2)
∴ Total amount Rohan have = [(3xy2)+(5xy2 + 10)] =Rs. [3xy2 + 5xy2 + 10]
= Rs. (8xy2 + 10)
Total amount spent by Rohan =Rs. (10 – 3xy2)
∴After spending, Rohan have left money
Question 85:

Solution:

Question 86:
The sum of first natural numbers is given by ½ n2 + ½ n.
(i) The sum of first 5 natural numbers.
(ii) The sum of first 11 natural numbers.
(iii) The sum of natural numbers from 11 to 30.
Solution:


Question 87:
The sum of squares of first n natural numbers is given by 1/6(n+1)(2n+1) or 1/6(2n3 + 3n2 + n). Find the sum of squares of the first 10 natural numbers.
Solution:
Given, the sum of squares of first n natural numbers = 1/6(n +1)(2n + 1)
∴ The sum of squares of first 10 natural numbers [∴ put n=10]
= 1/6 (10)(10+1)(2 x 10+1) =1/6 x 10 x 11 x 21
= 385
Question 88:
The sum of the multiplication table of natural number n is given by 55 x n. Find the sum of
(a) Table of 7 (b) Table of 10 (c) Table of 19
Solution:
Given, the sum of multiplication table of n natural numbers = 55 x n
(a) Sum of table of 7 = 55 x 7 =385 [put n = 7]
(b) Sum of table of 10=55 x 10=550 [put n = 10]
(c) Sum of table of 19 = 55 x 19=1045 [put n = 19]
Question 89:

Solution:


Question 90:

Solution:

Question 91:
4b – 3
Solution:
Three subtracted from four times b.
Question 92:
8(m+5)
Solution:
Eight times the sum of m and 5.
Question 93:
7/(8-x)
Solution:
Quotient on dividing seven by the difference of eight and x(x<8).
Question 94:
17(16/w)
Solution:
Seventeen times quotient of sixteen divided by w.
Question 95:
- Critical Thinking Write two different algebraic expressions for the word phrase (¼) of the sum of x and 7.
- What’s the Error? A student wrote an algebraic expression for “5 less than a number n divided by 3” as (n/3 )- 5. What error did the student make?
- Write About It Shashi used addition to solve a word problem about the weekly cost of commuting by toll tax for Rs. 15 each day. Ravi solved the same problem by multiplying. They both got correct answer. How is this possible?
Solution:
- First expression = ¼(x+7)
As we know, the addition is commutative.
So, it can also be written as = ¼ (7 + x) - Since, the expression of 5 less than a number n =n-5
So, 5 less than a number n divided by 3 will be written = (n-5)/3.
So, student make an error of quotient. - By addition method,
Total weekly cost = (15+15+15+15+15+15+15)
= Rs. 105
By multiplication method,
Total weekly cost = Cost of one day x Seven days =15 x 7 = Rs. 105
Question 96:
Challenge
Write an expression for the sum of 1 and twice a number n, if you let n be any odd number, will the result always be an odd number?
Solution:
Let the number be n.
So, according to the statement, the expression can be written as = 2n+1.
Yes, the result is always an odd number, because when a number becomes multiplied by 2, it becomes even and addition of 1 in that even number makes it an odd number.
Question 97:
Critical Thinking
Will the value of 11x for x – 5 be greater than 11 or less than 11? Explain.
Solution:
Expression given is
11x = 11 x (-5)= -55 [put x = —5]
Clearly, -55 <11.
Hence, the value is grater than 11.
Question 98:
Matching the column I and Column II by the following

Solution:

Question 99:
At age of 2 years, a cat or a dog is considered 24 “human” years old. Each year, after age 2 is equivalent to 4 “human” years. Fill in the expression [24+[] (a – 2)], so that it represents the age of a cat or dog in human years. Also, you need to determine for what ‘a’ stands for. Copy the chart and use your expression to complete it.

Solution:

Question 100:
Express the following properties with variables x, y and z.
- Commutative property of addition
- Commutative property of multiplication
- Associative property of addition
- Associative property of multiplication
- Distributive property of multiplication over addition
Solution:
- We know that,
Commutative property of addition, a + b = b + c
∴ Required expression is x + y=y + x - We know that,
Commutative property of multiplication, axb = bxa
∴ Required expression is x x y=y x x - We know that,
Associative property of addition, a + (b + c) = (a + b) + c
∴ Required expression is x + (y+ z)=(x+ y)+ z - We know that,
Associative property of multiplication, a x (b x c) = (a x b)x c
∴ Required expression is x x (y x z)=(x x y)x z - We know that,
Distributive property of multiplication over
addition, ax(b + c) = a x b + a x c
∴ Required expression is x x(y+ z)= x x y + x x z
NCERT Exemplar ProblemsNCERT Exemplar MathsNCERT Exemplar Science