With new discoveries and innovations constantly being made, the study of Physics Topics remains a vibrant and exciting field of research.
Kepler’s Law of Planetary Motions – Definition, Diagrams
Johannes Kepler was a 16th century astronomer who established three laws which govern the motion of planets (around the sun). These are known as Kepler’s laws of planetary motion. The same laws also describe the motion of satellites (like the moon) around the planets (like the earth). The Kepler’s laws of planetary motion are given on the next page.

1. Kepler’s first law states that: The planets move in elliptical orbits around the sun, with the sun at one of the two foci of the elliptical orbit. This law means that the orbit (or path) of a planet around the sun is an ellipse (oval-shaped) and not an exact circle. An elliptical path has two foci, and the sun is at one of the two foci of the elliptical path (foci is the plural of focus). This is shown in Figure 15. In Figure, a planet P is moving around the sun S in an elliptical orbit. The elliptical orbit has two foci F1 and F2. The sun is situated at the focus F1 (see Figure).
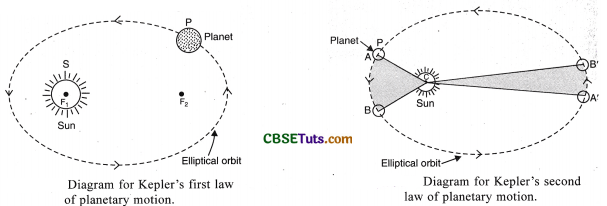
2. Kepler’s second law states that : Each planet revolves around the sun in such a way that the line joining the planet to the sun sweeps over equal areas in equal intervals of time. We know that a planet moves around the sun in an elliptical orbit with sun at one of its focus. Now, since the line joining the planet and the sun sweeps over equal areas in equal intervals of time, it means that a planet moves faster when it is closer to the sun, and moves slowly when it is farther from the sun. This point will become more clear from Figure.
In Figure, a planet P is moving in an elliptical orbit around the sun. When the planet is nearer to the sun at position A, it travels faster and sweeps over an area ABC in time t. On the other hand, when the same planet is farther from the sun at position A’, then it moves slowly but sweeps over an equal area A’B’C in the same time t. Thus, the Kepler’s second law tells us that a planet does not move with constant speed around the sun. The speed is greater when the planet is nearer the sun, and less when the planet is farther away from the sun. A planet could move around the sun with constant speed only if its orbit were a true circle (and not an ellipse).
3. Kepler’s third law states that: The cube of the mean distance of a planet from the sun is directly proportional to the square of time it takes to move around the sun. This law can be expressed as :
r3 ∝ T2
or r3 = constant × T2
or \(\frac{r^3}{T^2}\) = constant
where r = mean distance of planet from the sun
T = time period of the planet (around the sun)
Though Kepler gave the laws of planetary motion but he could not give a theory to explain the motion of planets. It was Newton who showed that the cause of the motion of planets is the gravitational force which the sun exerts on them. In fact, Newton used the Kepler’s third law of planetary motion to develop the law of universal gravitation. This is discussed below.
How Did Newton Guess the Inverse-Square Rule
The statement made by Newton in his universal law of gravitation that ‘the force between two bodies is inversely proportional to the square of distance between them’ is called the inverse-square rule. That is, the inverse-square rule is :
F ∝ \(\frac{1}{r^2}\)
Newton got the idea of the inverse-square rule for gravitational force between two bodies by applying Kepler’s third law to the orbit of a planet around the sun. An important assumption made for this purpose is that the orbit of a planet around the sun is ‘circular’. Newton derived the inverse-square rule for gravitational force as follows.
Consider a planet of mass m moving with a velocity (or speed) v around the sun in a circular orbit of radius r. A centripetal force F acts on the orbiting planet (due to the sun) which is given by :
F = \(\frac{m v^2}{r}\)
Since the mass m of a given planet is constant, so we can write the above equation as :
F ∝ \(\frac{v^2}{r}\) ……. (1)
Now, if the planet takes time T to complete one revolution (of 2πr) around the sun, then its velocity v is given by:
v = \(\frac{2 \pi r}{T}\)
Here the factor 2π is a constant, so we can write this equation as :
v ∝ \(\frac{r}{T}\)
Now, taking square on both sides, we get:
v2 ∝ \(\frac{r^2}{T^2}\)
If we multiply as well as divide the right side of this relation by r, we get:
v2 ∝ \(\frac{r^3}{T^2} \times \frac{1}{r}\)
Now, by Kepler’s third law of planetary motion, the factor \(\frac{r^3}{T^2}\) is constant. So, the above relation becomes
v2 ∝ \(\frac{1}{r}\) ……(2)
By putting \(\frac{1}{r}\) in place of v2 in relation (1), we get :
F ∝ \(\frac{1}{r \times r}\)
or F ∝ \(\frac{1}{r^2}\)
Thus, the gravitational force between the sun and a planet is inversely proportional to the square of distance between them. It was this conclusion obtained by using Kepler’s third law of planetary motion which helped Newton to formulate universal law of gravitation.