NCERT Solutions for Class 9 Maths Chapter 11 Constructions Ex 11.1

NCERT Solutions for Class 9 Maths Chapter 11 Constructions 11.1 are part of NCERT Solutions for Class 9 Maths. Here we have given NCERT Solutions for Class 9 Maths Chapter 11 Constructions Ex 11.1.

• Constructions Class 9 Ex 11.1
• Constructions Class 9 Ex 11.2

Board	CBSE
Textbook	NCERT
Class	Class 9
Subject	Maths
Chapter	Chapter 11
Chapter Name	Constructions
Exercise	Ex 11.1
Number of Questions Solved	5
Category	NCERT Solutions

NCERT Solutions for Class 9 Maths Chapter 11 Constructions Ex 11.1

Ex 11.1 Class 9 Maths Question 1.
Construct an angle of 90° at the initial point of a given ray and justify the construction.
Solution:
Steps of construction

(i) First, draw a ray OA with initial point 0.
(ii) Taking O as center and some radius, draw an arc of a circle which intersects OA at a point B (say).
(iii) Taking B as center and with the same radius as before, draw an arc intersecting the previous arc at a point C (say).
(iv) Taking C as center and with the same radius as before, draw an arc intersecting the arc drawn in step (ii) at D (say).
(v) Draw the ray OE passing through C, then ∠EOA = 60° and the ray OF
passing through D, then ∠FOE = 60°.
(vi) Next taking C and D as centers and with the radius more than \(\cfrac { 1 }{ 2 } \) CD, draw arcs to intersect each other at a point G (say).
Draw the ray OG, which is the angle bisector of the ∠FOE.
i.e., ∠FOG = ∠GOE = \(\cfrac { 1 }{ 2 } \)∠FOE = \(\cfrac { 1 }{ 2 } \) (60°) = 30°
Thus, ∠GOA = ∠GOE +∠EOA = 30° + 60° = 90°
Hence, ∠GOA is the required angle of 90°.
Justification

Ex 11.1 Class 9 Maths Question 2.
Construct an angle of 45° at the initial point of a given ray and justify the construction.
Solution:
Steps of construction
(i) Taking O as center and some radius, draw an arc of a circle which intersects OA, say at a point ‘
(ii) Taking B as center and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.

(iii) Taking C as center and with the same radius as before, draw an arc intersecting the arc drawn in step (i) say at D.
(iv) Draw the ray OE passing through C. Then, ∠EOA = 60°.
(v) Draw the ray OF passing through D. Then, ∠FOE = 60°.
(vii) Next, taking C and D as centers and with radius more than – CD, draw arcs to intersect each other, say at G.
(vii) Draw the ray OG. This ray OG is the bisector of the ∠FOE, i.e., ∠FOG
= ∠EOG = \(\cfrac { 1 }{ 2 } \) ∠FOE = \(\cfrac { 1 }{ 2 } \) (60° ) = 30°.
Thus,  ∠GOA = ∠GOE + ∠EOA
= 30°+ 60° = 90°
(viii) Now taking O as center and any radius, draw an arc to intersect the rays OA and OG, say at H and I, respectively.
(ix) Next, taking H and 1 as centers and with the radius more than \(\cfrac { 1 }{ 2 } \) HI, drawarcs to intersect each other, say at J.
(x) Draw the ray OJ. This ray OJ is the required bisector of the ∠GOA.


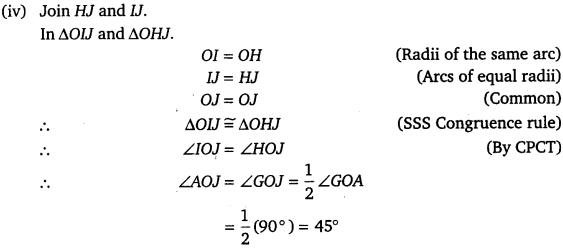
Ex 11.1 Class 9 Maths Question 3.
Construct the angles of the following measurements :
(a) 30°
(b) 22 \(\cfrac { 1 }{ 2 } \)°
(c) 15°
Solution:
(a) Steps of construction

(i) First, draw a ray OA with initial point O.
(ii) Taking O as center and some radius, draw an arc of a circle which insects OA at a point B (say). Taking B as center and with the same radius as before, draw an arc intersecting the previously drawn arc at a point C (say).
(iii) Draw the ray OE passing through C. Then, ∠EOA = 60°
(iv) Taking B and C as centers and with the radius more than \(\cfrac { 1 }{ 2 } \) BC, draw arcs to intersect each other at a point D (say).
(v) Draw the ray OD, which is the bisector of the ∠EOA.
i.e.,  ∠EOD = ∠AOD = – ∠EOA = -(60°) = 30°
Hence, ∠AOD is the required angle of 30°.
(b) Here, 22 \(\cfrac { 1 }{ 2 } \) = \(\cfrac { 45 }{ 2 } \) . So, to draw an angle of 22 \(\cfrac { 1 }{ 2 } \), firstly draw an angle of 90° and bisect it to get an angle of 45°. Again, bisect an angle of 45° to get 1° required angle of 22 \(\cfrac { 1 }{ 2 } \).

Steps of Constraction

(i) First, draw a ray OA with initial point O.
(ii) Taking 0 as center and any radius, draw an arc of a circle which intersects OA at a point say B
(iii) Taking B as center and with the same radius as before, draw an arc intersecting the previously drawn arc at a point say C.
(iv) Taking C as center and with the same radius as  before, draw an arc intersecting the arc drawn in step (ii) at a point say D.
(v) Draw the ray OE passing through C and the ray OF passing through Then, ∠EOA = 60° and
∠FOE = 60°.
(vi) Next, taking C and D as centers and with radius more than \(\cfrac { 1 }{ 2 } \) CD, draw arcs to intersect each other at a point say G.
(vii) Draw the ray OG, which is the angle bisector of the
i.e. ∠FOG = ∠GOE = \(\cfrac { 1 }{ 2 } \) ∠FOE = \(\cfrac { 1 }{ 2 }\) (60° ) = 30°
Thus ∠GOA = ∠GOE + ∠EOA = 30° + 60° = 90°
(viii) Now, taking O as center and any radius, more than OB, draw an arc to intersect the rays OA and OG, say at H and I, respectively.
(ix) Next, taking H and I as centers and with the radius more than \(\cfrac { 1 }{ 2 } \) HI, draw arcs to intersect each other, say at J.|
(x) Draw the ray OJ, which is the angle bisector of the
∠GOJ = ∠AOJ = \(\cfrac { 1 }{ 2 } \) ∠GOA = \(\cfrac { 1 }{ 2 } \) (90°) = 45°
(xi) Now, taking O as centre and any radius more than OH, draw an arc to intersect the rays OA and OJ, say at K and L, respectively.
(xii) Next, taking K and L as centers and with the radius more than \(\cfrac { 1 }{ 2 } \) KL, draw arcs to intersect each other, say at M.
(xiii) Draw the ray OM, which is the angle bisector of the ∠AOJ.
∠JOM = ∠AOM = \(\cfrac { 1 }{ 2 } \) ∠AOJ = \(\cfrac { 1 }{ 2 } \) (45° ) = 22
Hence, ∠AOM is the required angle of 22\(\cfrac { 1 }{ 2 } \)
(c)  Here \(\cfrac { { 30 }^{ o } }{ 2 } \) = \( \cfrac { { 60 }^{ o }/2 }{ 2 } \)  =\(\cfrac { { 60 }^{ o } }{ 2 } \) . So to draw an angle of 15°, firstly we draw an angle of 60°, then bisect it to get an angle of 30°. Again, bisect an angle of 30° to get required angle of 15°.

Steps of construction

(i) First, draw a ray OA with initial point O.
(ii) Taking O as center and any radius, draw an arc of a circle which intersects OA at a point say
(iii) Taking B as center and with the same radius as before, draw an arc intersecting the previously drawn arc at a point say C.
(iv) Draw the ray OE passing through C. Then, ∠EOA = 60°.
(v) Now, taking B and C as centers and with the radius more than \(\cfrac { 1 }{ 2 } \) BC, draw arcs to intersect each other, say at
(vi) Draw the ray OD intersecting the arc drawn in step (ii) at F. This ray OD is the angle bisector of the
∠EOD = ∠AOD = \(\cfrac { 1 }{ 2 } \) ∠EOA = \(\cfrac { 1 }{ 2 } \) (60° ) = 30^°
(vii) Now, taking B and F as centers and with the radius more than \(\cfrac { 1 }{ 2 } \) BF, draw arcs to intersect each other, say at G.
(viii) Draw the ray 0G, which is the angle bisector of the ∠AOD.
∠DOG = ∠AOG = \(\cfrac { 1 }{ 2 } \) ∠AOD =\(\cfrac { 1 }{ 2 } \) (30°) = 15°
Hence, ∠AOG is the required angle of 15°.

Ex 11.1 Class 9 Maths Question 4.
Construct the following angles and verify by measuring them by a protractor:
(i) 75°
(ii) 105°
(iii) 135°
Solution:
(i) Steps of construction

1. Taking O as center and some radius, draw an arc of a circle which intersects OA, say at a point B.
2. Taking B as center and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
3. Taking C as centro and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
4. Join the ray OE passing through C. Then, ∠EOA = 60°
5. Draw the ray OF passing through D. Then, ∠FOE = 60°.
6. Next taking C and D as centers and with the radius more than \(\cfrac { 1 }{ 2 } \) CD, draw arcs to intersect each other, say at G.
7. Draw the ray OG intersecting the arc of step (1) at H. This ray OG is bisector of the ∠FOE,
   i.e… ∠FOG = ∠EOG
   = \(\cfrac { 1 }{ 2 } \)FOE = \(\cfrac { 1 }{ 2 } \) (60°)  =  (60°)
8. Next, taking C and H as centers and with the radius more than \(\cfrac { 1 }{ 2 } \) CH, draw
9. arcs to intersect each other, say at I.
10. Draw the ray OI. This ray OI is the bisector of the ∠GOE,
11. i.e., ∠GOI = ∠EOI = \(\cfrac { 1 }{ 2 } \)∠GOE = \(\cfrac { 1 }{ 2 } \) (30° ) = 15°
    Thus,    ∠IOA = ∠IOE + ∠EOA
    = 15° +60° =75°
    On measuring the ∠IOA by protractor, we find that ∠IOA = 75° Thus, the construction is verified.

(ii) Steps of construction

1. Taking O as center and some radius, draw an arc of a circle which intersects OA, say at a point B.
2. Taking B as center and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
3. Taking C as center and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at a point D.
4. Draw the ray OE passing through C. Then, ∠EOA = 60°.
5. Draw the ray OF passing through D. Then, ∠FOE = 60°
6. Next, taking C and D as centers and with the radius more than \(\cfrac { 1 }{ 2 } \) CD,’ draw arcs to intersect each other, say at G.
7. Draw the ray OG intersecting the arc of step 1 at H. This ray OG is the bisector of the ∠FOE, i.e.,
   ∠FOG = ∠EOG = \(\cfrac { 1 }{ 2 } \) ∠FOE
   = \(\cfrac { 1 }{ 2 } \) (60°) = 30°
   Thus, ∠GOA = ∠GOE + ∠EOA
   = 30°+60° = 90°
8. Next, taking H and D as centers and with the radius more than -HD, draw arcs to intersect each other, say at I.
9. Draw the ray OI. This ray OI is the bisector of the ∠FOG,
   i.e.. ∠FOI = ∠GOI = \(\cfrac { 1 }{ 2 } \) ∠FOG = \(\cfrac { 1 }{ 2 } \) (30°) = 15°.
   Thus  ∠IOA= ∠IOG + ∠GOA
   = 15°+90° = 105°
   On measuring the ∠IOA by protractor, we find that ∠IOA = 105° Thus, the construction is verified.

(iii) Steps of construction

1. Produce AO to A’ to form ray OA’.
2. Taking O as a center and some radius, draw an arc of a circle which intersects OA at a point B and OA’ at a point B’.
3. Taking B as center and with the same radius as before, draw an arc intersecting the previously drawn arc at a point C.
4. Taking C as center and with the same radius as before, draw an arc intersecting the arc drawn in step 1, say at D.
5. Draw the ray OE passing through C. Then, ∠EOA = 60°.
6. Draw the ray OF passing through D. Then, ∠FOE = 60°.
7. Next, taking C and D as centers and with the radius more than \(\cfrac { 1 }{ 2 } \) CD, draw arcs to intersect each other, say at G.
8. Draw the ray OG intersecting the arc of step 1 at H. This ray OG is bisector of the ∠FOE, i.e.,
   ∠FOG = ∠EOG = \(\cfrac { 1 }{ 2 } \) ∠FOE = \(\cfrac { 1 }{ 2 } \) (60° ) = 30°
   Thus, ∠GOA = ∠GOE + ∠EOA
   = 30° + 60° = 90°
   ∴  ∠B’OH = 90°
9. Next, taking B’ and H as centers and with the radius more than \(\cfrac { 1 }{ 2 } \) B’H,draw arcs to intersect each other, say at I.
10. Draw the Ray Ol. This ray Ol is the bisector of the ∠B’OG,
    i..e,∠B’0I = ∠GOI
    = \(\cfrac { 1 }{ 2 } \) ∠B’OG = \(\cfrac { 1 }{ 2 } \) (90°) = 45°
    Thus, ∠IOA = ∠IOG + ∠GOA
    = 45° + 90° +135°
    On measuring the ∠IOA by protractor, we find that ∠IOA = 135°
    Thus, the construction is verified.

Ex 11.1 Class 9 Maths Question 5.
Construct an equilateral triangle, given its side and justify the construction.
Solution:
Steps of construction

(i) First, draw a ray AX with initial point A.
(ii) Taking A as a center and same radius (say 4 cm), draw an arc of a circle, which intersects AX at point B.
(iii) Taking B as center and with the same radius as before, draw an arc intersecting the previously drawn arc, say at a point C.
(iv) Join AC and BC.
Thus, Δ ABC is an equilateral triangle.
Justification
In Δ ABC,
AB = BC  [ radii of same circle]
AB = AC [ radii of same circle]
∴  AB = BC = CA
So, Δ ABC is an equilateral triangle.
Hence, the construction is justified.

We hope the NCERT Solutions for Class 9 Maths Chapter 11 Constructions Ex 11.1 help you. If you have any query regarding NCERT Solutions for Class 9 Maths Chapter 11 Constructions 11.1, drop a comment below and we will get back to you at the earliest.