Selina Concise Mathematics Class 6 ICSE Solutions Chapter 24 Angles

Selina Concise Mathematics Class 6 ICSE Solutions Chapter 24 Angles (With their Types)

Selina Publishers Concise Mathematics Class 6 ICSE Solutions Chapter 24 Angles (With their Types)

Angles Exercise 24A – Selina Concise Mathematics Class 6 ICSE Solutions

Question 1.
For each angle given below, write the name of the vertex, the names of the arms and the name of the angle.

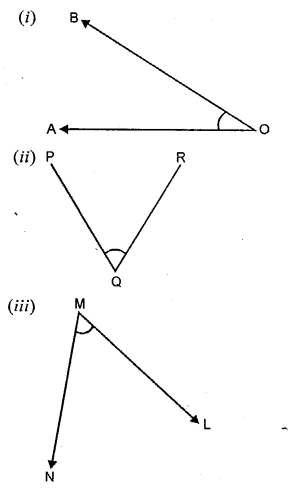
Solution:

Question 2.
Name the points :
(i) in the interior of the angle PQR,
(ii) in the exterior of the angle PQR.

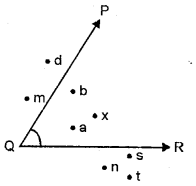
Solution:

Question 3.
In the given figure, figure out the number of angles formed within the arms OA and OE.

Solution:

Question 4.
Add :
(i) 29° 16′ 23″ and 8° 27′ 12″
(ii) 9° 45’56” and 73° 8′ 15″
(m) 56° 38′ and 27° 42’30”
(iv) 47° and 61° 17’4″
Solution:

Question 5.
In the figure, given below name :
(i) three pairs of adjacent angles.
(ii) two acute angles,
(iii) two obtuse angles
(iv) two reflex angles.

Solution:

Question 6.
In the given figure ; PQR is a straight line. If :
(i) ∠SQR = 75° ; find ∠PQS.
(ii) ∠PQS = 110°; find ∠RQS

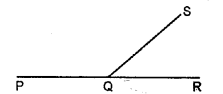
Solution:

Question 7.
In the given figure ; AOC-is a straight line. If angle AOB = 50°, angle AOE = 90° and angle COD = 25° ; find the measure of :
(i) angle BOC
(ii) angle EOD
(iii) obtuse angle BOD
(iv) reflex angle BOD
(v) reflex angle COE.

Solution:

Question 8.
In the given figure if :
(i) a = 130° ; find b.
(ii) b = 200 ; find a.
(iii) a = 5/3 right angle, find b

Solution:

Question 9.
In the given diagram, ABC is a straight line.
(i) If x = 53°, find y.
(ii) If y =1 right angles ; find x.

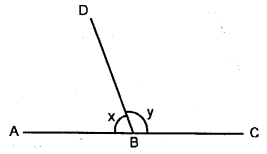
Solution:

Question 10.
In the given figure, AOB is a straight line. Find the value ofx and also answer each of the following :
(i) ∠AOP = ……..
(ii) ∠BOP = ……..
(iii) which angle is obtuse ?
(iv) which angle is acute ?

Solution:

Question 11.
In the given figure, PQR is a straight line. Find x. Then complete the following:
(i) ∠AQB = ……..
(ii) ∠BQP = ……..
(iii) ∠AQR = …….

Solution:

Question 12.
In the given figure, lines AB and CD intersect at point O.
(i) Find the value of ∠a.
(ii) Name all the pairs of vertically opposite angles.
(iii) Name all the pairs of adjacent angles.
(iv) Name all the reflex angles formed and write the measure of each.

Solution:

Question 13.
In the given figure :
(i) If ∠AOB = 45°, ∠BOC = 30° and ∠AOD= 110°;
find : angles COD and BOD.
(ii) If ∠BOC = ∠DOC = 34° and ∠AOD = 120° ;
find : angle AOB and angle AOC.
(iii) If ∠AOB = ∠BOC = ∠COD = 38°
find : reflex angle AOC and reflex angle AOD.

Solution:

Angles Exercise 24B – Selina Concise Mathematics Class 6 ICSE Solutions

Question 1.
Write the complement angle of :
(i) 45°
(ii) x°
(iii) (x – 10)°
(iv) 20° + y°
Solution:

Question 2.
Write the supplement angle of :
(i) 49°
(ii) 111°
(iii) (x – 30)°
(iv) 20° + y°
Solution:

Question 3.
Write the complement angle of :


Solution:

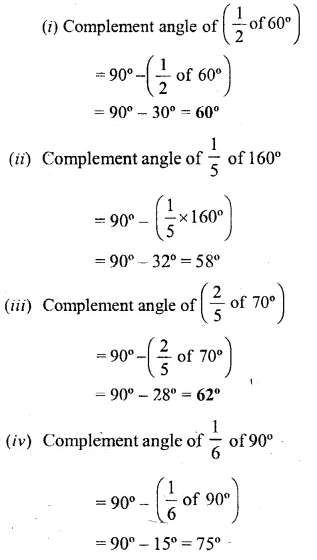
Question 4.

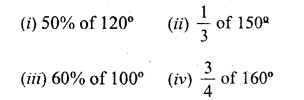
Solution:

Question 5.
Find the angle :
(i) that is equal to its complement ?
(ii) that is equal to its supplement ?
Solution:

Question 6.
Two complementary angles are in the ratio 7 : 8. Find the angles.
Solution:

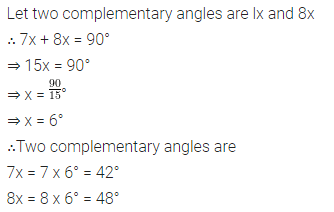
Question 7.
Two supplementary angles are in the ratio 7 : 11. Find the angles.
Solution:

Question 8.
The measures of two complementary angles are (2x – 7)° and (x + 4)°. Find x.
Solution:

Question 9.
The measures of two supplementary angles are (3x + 15)° and (2x + 5)°. Find x.
Solution:

Question 10.
For an angle x°, find :
(i) the complementary angle
(ii) the supplementary angle
(iii) the value of x° if its supplementary angle is three times its complementary angle.
Solution:

Angles Revision Exercise – Selina Concise Mathematics Class 6 ICSE Solutions

Question 1.
Explain what do you understand by :
(i) Adjacent angles ?
(ii) Complementary angles ?
(iii) Supplementary angles ?
Solution:

Question 2.
Find the value of ‘x’ for each of the following figures :


Solution:

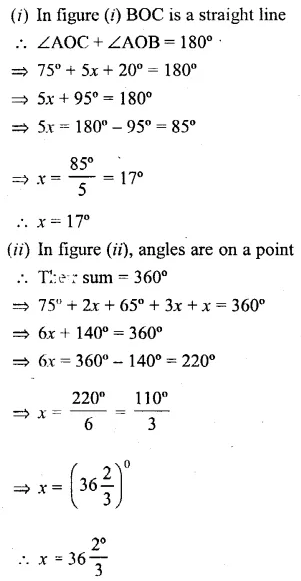
Question 3.
Find the number of degrees in an angle that is (i) of a right angle (ii) 0.2 times of a straight line angle.
Solution:

Question 4.
In the given figure; AB, CD and EF are straight lines. Name the pair of angles forming :
(i) straight line angles.
(ii) vertically opposite angles.

Solution:

Question 5.
Find the complement of :

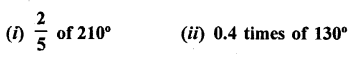
Solution:

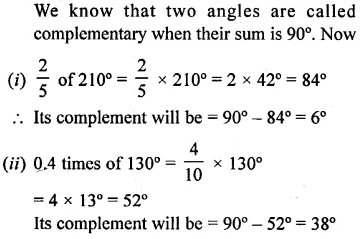
Question 6.
Find the supplement of :

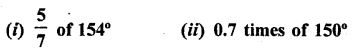
Solution:

Question 7.
Two complementary angles are in the ratio 8 : 7. Find the angles.
Solution:

Question 8.
Two supplementary angles are in the ratio 7 : 5. Find the angles.
Solution:

Question 9.
Two supplementary angles are (5x – 82°) and (4x + 73°). Find the value of x.
Solution:

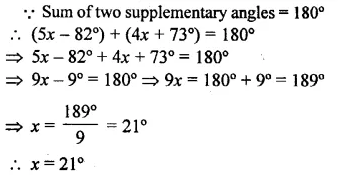
Question 10.
Find the angle formed by the arms of a clock at:
(i) 3 O’clock
(ii) 6 O’clock
(iii) 9 O’clock
(iv) 12 O’clock
Solution:

Question 11.
For an angle y°, find :
(i) its supplementary angle.
(ii) its complementary angle.
(iii) the value of y° if its supplement is four times its complement.
Solution:

Question 12.
Use the adjoining figure to find :
(i) ∠BOD
(ii) ∠AOC
Solution:

Question 13.
Two adjacent angles forming a linear pair are in the ratio 7:5, find the angles.
Solution:

Question 14.
Find the angle that is three times its complementary angle.
Solution:

Question 15.
An angle is one-thirds of a straight line angle ; find :
(i) the angle
(ii) the complement and the supplement of the angle obtained above.
Solution:

Selina Concise Mathematics Class 6 ICSE Solutions