Speed – Definition, Formula, Units and Solved Examples

Physics Topics can help us understand the behavior of the natural world around us.

What is Formula For Speed ? And Define Average Speed and Constant Speed

The motion of a body can be described by three terms : Speed, Velocity and Acceleration. Let us study them in detail, one by one.

If a car is running slow, we say that its speed is low. And if a car is running fast, then we say that its speed is high. Thus, the speed of a body gives us an idea of how slow or fast that body is moving. We can now define the speed of a moving body as follows :

Speed of a body is the distance travelled by it per unit time. The speed of a body can be calculated by dividing the ‘Distance travelled’ by the ‘Time taken’ to travel this distance. So, the formula for speed can be written as :

Speed = \(\frac{\text { Distance travelled }}{\text { Time taken }}\)
If a body travels a distance s in time t, then its speed v is given by :
v = \(\frac{s}{t}\)
where v = speed
s = distance travelled
and t = time taken (to travel that distance)
Suppose a car travels a distance of 100 kilometres in 4 hours, then the speed of this car is given by :
SPeed = \(\frac{100 \text { kilometres }}{4 \text { hours }}\)
Speed = 25 kilometres per hour (or 25 km/h)

Thus, the speed of this car will be 25 kilometres per hour. This means that the car travels a distance of 25 kilometres ‘every one hour’. The above given formula for calculating speed has three quantities in it : Speed, Distance travelled and Time taken. If we are given the values of any two quantities, then the value of third quantity can be calculated by using this formula.

The SI unit of distance is metre (m) and that of time is second (s), therefore, the SI unit of speed is metres per second which is written as m/s or ms^-1. The small values of speed are expressed in the units of centimetres per second which is written as cm/s or cm s^-1.

To express high speed values, we use the unit of kilometres per hour, written as km.p.h. or km/h or km h^-1. Please note that if we have to compare the speeds of a number of bodies, then we must express the speeds of all of them in the same units. Speed has magnitude only, it has no specified direction, therefore, speed is a scalar quantity.

The speed of a running car at any instant of time is shown by an instrument called ‘speedometer’ which is fixed in the car. The speedometer gives the speed in kilometres per hour. The distance travelled by a car is measured by another instrument called ‘odometer’ which is also installed in the car. It records the distance in kilometres.

Average Speed

The average speed of a body is the total distance travelled divided by the total time taken to cover this distance. While travelling in a car (or a bus) we have noticed that it is very difficult to keep the speed of the car at a constant or uniform value because at many places the brakes are to be applied to slow down or stop the car due to various reasons.

Thus, the speed of a body is usually not constant and the distance travelled divided by time gives us the average speed during that time. For example, for a car which travels a distance of 100 km in 4 hours, the average speed is \(\frac{100}{4}\) = 25 km per hour. Although the average speed of this car is 25 km per hour, it does not mean that the car is moving at this speed all the time.

When the road is straight, flat and free, the speed may be much more than 25 km per hour but on bends (curved road), hills or in a crowded area, the speed may fall well below this average value. We should remember that:
Average Speed = \(\frac{\text { Total distance travelled }}{\text { Total time taken }}\)

We will use this formula for solving numerical problems after a while. The average speeds of some of the moving objects are given below.

Uniform Speed (or Constant Speed)

A body has a uniform speed if it travels equal distances in equal intervals of time, no matter how small these time intervals may be. For example, a car is said to have uniform speed of say, 60 km per hour, if it travels 30 km every half hour, 15 km every quarter of an hour, 1 km every minute, and \(\frac{1}{60}\) km every second. As we have already discussed above, in actual practice the speed of a body rarely remains uniform (or constant) for a long time. If, however, the speed of a body is known to be constant, we can find out exactly how much distance it will travel in a given time or if we know the distance travelled by the body, we can calculate the time taken to travel that distance. We will now solve some numerical problems based on speed.

Example Problem 1.
A scooterist covers a distance of 3 kilometres in 5 minutes. Calculate his speed in :
(a) centimetres per second (cm/s)
(b) metres-per second (m/s)
(c) kilometres per hour (km/h)
Solution:
(a) In order to calculate the speed in centimetres per second we should convert the given distance of 3 kilometres into centimetres and the given time of 5 minutes into seconds. Please note that 1 kilometre has 1000 metres and 1 metre has 100 centimetres. Now,
Distance travelled = 3 km
= 3 × 1000 m
= 3 × 1000 × 100 cm
= 300,000 cm ………. (1)
Time taken = 5 minutes
= 5 × 60 seconds
= 300 s ………… (2)
We know that, Speed = \(\frac{\text { Distance travelled }}{\text { Time taken }}\)
= \(\frac{300,000 \mathrm{~cm}}{300 \mathrm{~s}}\)
= 1000 cm/s …………. (3)
Thus, the speed of scooterist is 1000 centimetres per second.

(b) In order to express the speed in metres per second we should convert the given distance of 3 kilometres into metres and the given time of 5 minutes into seconds. Thus, in this case :
Distance travelled = 3 km
= 3 × 1000 m
= 3000 m ……….. (4)
Time taken = 5 minutes
= 5 × 60 seconds
= 300 s …………… (5)
Now, Speed = \(\frac{\text { Distance travelled }}{\text { Time taken }}\)
= \(\frac{3000 \mathrm{~m}}{300 \mathrm{~s}}\)
= 10 m/s …………… (6)
So, the speed of scooterist is 10 metres per second.

(c) And finally, in order to calculate the speed in kilometres per hour, we should express the given distance in kilometres (which is already so), and the given time in hours. So, in this case:
Distance travelled = 3 km …. (7)
Time taken = 5 minutes
= \(\frac{5}{60}\) hours
= 0.083 h ………. (8)
We know that, Speed = \(\frac{\text { Distance travelled }}{\text { Time taken }}\)
= \(\frac{3 \mathrm{~km}}{0.083 \mathrm{~h}}\)
= 36 km/h
Thus, the speed of scooterist is 36 kilometres per hour.

Example Problem 2.
The train ‘A’ travelled a distance of 120 km in 3 hours whereas another train ‘B’ travelled a distance of 180 km in 4 hours. Which train travelled faster ?
Solution:
In order to solve this problem, we have to calculate the speeds of both the trains separately. The train having higher speed will have travelled faster.
(i) We know that : Speed = \(\frac{\text { Distance travelled }}{\text { Time taken }}\)
Now, Distance travelled by train A = 120 km
And, Time taken by train A = 3 h
So, Speed of train A = \(\frac{120 \mathrm{~km}}{3 \mathrm{~h}}\)
= 40 km/h
Thus, the speed of train A is 40 kilometres per hour.

(ii) Again, Speed = \(\frac{\text { Distance travelled }}{\text { Time taken }}\)
Now, Distance travelled by train B = 180 km
And, Time taken by train B = 4 h
So, Speed of train B = \(\frac{180 \mathrm{~km}}{4 \mathrm{~h}}\)
= 45 km/h
Thus, the speed of train B is 45 kilometres per hour.

From the above calculations we find that the train A travels a distance of 40 kilometres in one hour whereas the train B travels a distance of 45 kilometres in one hour. Since the speed of train B is higher, therefore, train B has travelled faster.

Example Problem 3.
A car travels 30 km at a uniform speed of 40 km/h and the next 30 km at a uniform speed of 20 km/h. Find its average speed.
Solution:
(i) First the car travels a distance of 30 kilometres at a speed of 40 kilometres per hour. Let us find out the time taken by the car to travel this distance.
Here, Speed = 40 km/h
Distance = 30 km
And, Time = ? (To be calculated)
We know that, Speed = \(\frac{\text { Distance }}{\text { Time }}\)
So, 40 = \(\frac{30}{\text { Time }}\)
And, Time = \(\frac{30}{40}\) hours
Or Time (t₁) = \(\frac{3}{4}\) hours

(ii) Next the car travels a distance of 30 km at a speed of 20 km/h. We will also find out the time taken by the car to travel this distance. In this case :
Speed = 20 km/h
Distance = 30 km
And, Time = ? (To be calculated)
Again, Speed = \(\frac{\text { Distance }}{\text { Time }}\)
So, 20 = \(\frac{30}{\text { Time }}\)
And, Time = \(\frac{30}{20}\) hours
Or, Time (t₂) = \(\frac{3}{2}\) hours
We can get the total time taken by the car for the whole journey by adding the above two time values t₁ and t₂. Thus,
Total time taken = \(\frac{3}{4}\) + \(\frac{3}{2}\) hours
= \(\frac{3+6}{4}\) hours
= \(\frac{9}{4}\) hours
And, Total distance travelled = 30 km + 30 km
= 60 km
Now, Average speed = \(\frac{\text { Total distance travelled }}{\text { Total time taken }}\)
= \(\frac{60 \times 4}{9}\)
= \(\frac{240}{9}\)
= 26.6 km/h
Thus, the average speed of the car for the whole journey is 26.6 kilometres per hour.

Example Problem 4.
On a 120 km track, a train travels the first 30 km at a uniform speed of 30 km/h. How fast must the train travel the next 90 km so as to average 60 km/h for the entire trip ?
Solution:
In this numerical problem we have been given the total distance travelled by the train (which is 120 km), and the average speed of the train for the whole journey (which is 60 km/h). From these two values we can calculate the total time taken by the train for the entire journey. This can be done as follows :
We know that, Average speed = \(\frac{\text { Total distance travelled }}{\text { Total time taken }}\)
So, 60 = \(\frac{120}{\text { Total time taken }}\)
And, Total time taken = \(\frac{120}{60}\) hours
= 2 hours

We will now calculate the time taken by the train for the first 30 km journey, and the next 90 km journey, separately (see Figure).
(i) For the first part of the train journey, we have :
Speed= 30 km/h
Distance = 30 km
And, Time = ? (To be calculated)
Now, Speed = \(\frac{\text { Distance travelled }}{\text { Time taken }}\)
So, 30 = \(\frac{30}{\text { Time taken }}\)
And, Time taken = \(\frac{30}{30}\) hours
= 1 hour

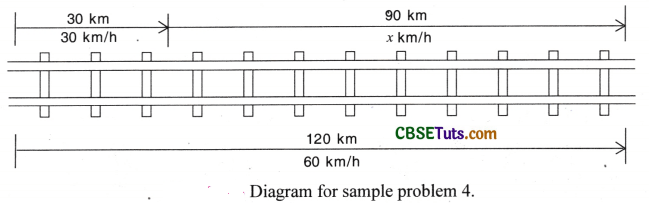
(ii) For the second part of the train journey, let us suppose that the speed of the train is x km/h. So, for the second part of the train journey, we have :
Speed = x km/h (Supposed)
Distance = 90 km
And, Time = ? (To be calculated)
Now, Speed = \(\frac{\text { Distance travelled }}{\text { Time taken }}\)
So, x = \(\frac{90}{\text { Time taken }}\)
And, Time taken = \(\frac{90}{x}\) hours ……………… (3)
Now, adding equations (2) and (3), we get the total time taken for the entire trip :
Total time taken = 1 + \(\frac{90}{x}\) hours ……… (4)
We already know from equation (1) that the total time taken for the entire trip is 2 hours. So, comparing equations (4) and (1), we get:
1 + \(\frac{90}{x}\) = 2
\(\frac{90}{x}\) = 2 – 1
\(\frac{90}{x}\) = 1
And x = 90 km/h
Thus, the train should travel the next 90 km distance at a speed of 90 km/h.

Example Problem 5.
A train travels at a speed of 60 km/h for 0.52 h, at 30 km/h for the next 0.24 h and then at 70 km/h for the next 0.71 h. What is the average speed of the train ?
Solution:
In this problem, first of all we have to calculate the distances travelled by the train under three different conditions of speed and time. •
(i) In the first case, the train travels at a speed of 60 km/h for a time of 0.52 hours.
Now, Speed = \(\frac{\text { Distance }}{\text { Time }}\)
So, 60 = \(\frac{\text { Distance }}{0.52}\)
And, Distance = 60 × 0.52
= 31.2 km

(ii) In the second case, the train travels at a speed of 30 km/h for a time of 0.24 hours.
Now, Speed = \(\frac{\text { Distance }}{\text { Time }}\)
So, 30 = \(\frac{\text { Distance }}{0.24}\)
And, Distance = 30 × 0.24
= 7.2km

(iii) In the third case, the train travels at a speed of 70 km/h for a time of 0.71 hours.
Again, Speed = \(\frac{\text { Distance }}{\text { Time }}\)
So, 70 = \(\frac{\text { Distance }}{0.71}\)
And, Distance = 70 × 0.71
= 49.7 km …………. (3)
Now, from the equations (1), (2) and (3), we get:
Total distance travelled = 31.2 + 7.2 + 49.7
= 88.1 km ……… (4)
And, Total time taken = 0.52 + 0.24 + 0.71
= 1.47h ……………… (5)
We know that : Average speed = \(\frac{\text { Total distance travelled }}{\text { Total time taken }}\)
= \(\frac{88.1}{1.47}\)
= 59.9 km/h

Speed

Definition: The distance travelled by a body in unit time is called its speed.

Distance is always measured along the path travelled by the moving body, irrespective of whether the path is straight or curved. Hence, if a body travels a length l in time t,
speed (v) \(=\frac{\text { distance travelled }(l)}{\text { time taken }(t)}\)
Speed is a scalar quantity.

Unit and dimension of speed in different systems of units:

Units of speed \(=\frac{\text { unit of length of the path travelled }}{\text { unit of time }}\)

Dimension of speed \(=\frac{\text { dimension of distance }}{\text { dimension of time }}\) = \(\frac{L}{T}\) = LT^-1

Relation among different Units:

1 m ᐧ s^-1 = 100 cm ᐧ s^-1
In addition km ᐧ h^-1 is also widely used.
1 km ᐧ h^-1 = \(\frac{1000}{60 \times 60}\) m ᐧ s^-1 = \(\frac{5}{18}\) m ᐧ s^-1
For easy recall, 18 km ᐧ h^-1 = 5 ᐧ m^-1

Average speed: Speed of a body can be uniform or variable. When a body travels equal distances in equal intervals of time, its speed is uniform.

When distances travelled in equal intervals of time are unequal, the body moves with a variable speed.

For convenience, the average speed is often calculated in case of motion with variable speed.

Dividing the total distance travelled by the total time taken to travel the distance, we get the average speed.

Thus if l₁, l₂, l₃ are the distances travelled by an object in times t₁, t₂ and t₃ respectively then its average speed
\(=\frac{\text { total distance travelled }}{\text { total time taken to travel the distance }}\) = \(\frac{l_1+l_2+l_3}{t_1+t_2+t_3}\)
The average speed is not an average of speeds.

Instantaneous speed: Speed of a moving body at any instant is called its instantaneous speed.

Let us consider that a running train travels 10 m in 0.5 s. For the motion of a train, this 0.5 s time interval is very small. So, this interval of time maybe considered as an instant. Dividing the distance travelled by the train by that short interval of time gives the instantaneous speed of the train. Hence, the instantaneous speed of the train = \(\frac{10}{0.5}\) = 20 ᐧ m s^-1.

Definition: The instantaneous speed of a particle at a given point is the limiting value of the rate of the distance travelled with respect to a time, when the time interval tends to zero.

Following the rule of differential calculus, if Δt is the time in which the distance travelled is Δl, then instantaneous speed is
v_i = \(\lim _{\Delta t \rightarrow 0} \frac{\Delta l}{\Delta t}\) = \(\frac{d l}{d t}\)

where, l is the distance or location of the particle along its locus from a given fixed point.

For a body moving with uniform speed, the instantaneous speed at any instant is equal to the uniform speed.

For example, the speed of a moving car is measured by a speedometer. At any moment, the speedometer reads the instantaneous speed of the car. The pointer of the speedometer remains stationary when the car runs with uniform speed. That is, the instantaneous speed is equal to the uniform speed of the car. The speedometer fluctuates when the car moves with varying speed.

Distinction between overage and instantaneous speed:

Average speed	Instantaneous speed
The total distance covered by a body in a certain interval of time, divided by the time interval is the average speed.	The rate of infinitesimal distance covered with respect to the corresponding infinitesimal time, is the instantaneous speed.