Rate of Flow of a Liquid : Equation of Continuity

From the study of subatomic particles to the laws of motion, Physics Topics offer insights into the workings of the world around us.

What are 3 Forms of Energy in a Fluid?

Rate of flow of liquid: For streamline flow of a perfectly incompressible liquid, the amount of liquid flowing through any cross section of a tube in a given time interval remains constant.

The rate of flow of a liquid through a tube means the volume of liquid flowing through any cross section of the tube per second.

Suppose a liquid flows through a tube of cross sectional area α with a uniform velocity v [Fig.]. The volume of liquid flowing through any cross section of the tube per second is equal to the volume of a cylinder of length v and cross sectional area α.

∴ Volume of liquid flowing per second = the rate of flow of the liquid = velocity of flow × area of cross section of the tube
= vα
Therefore, the mass of liquid flowing per second
= velocity of flow × area of cross-section of the tube × density of the liquid = vαρ [ρ = density of the liquid]

Continuity of flow: For a streamline flow of a fluid (liquid or gas) through a tube, the mass of the fluid flowing per second through any cross section of the tube remains constant. This is known as the continuity of flow.

Equation of continuity: Let us consider two sections A and B of a tube having cross sectional areas α₁ and α₂ respectively. The velocities of the fluid at the sections A and B are v₁ and v₂, and its densities are ρ₁ and ρ₂ respectively [Fig.].

The mass of fluid flowing through section A per second = v₁α₁ρ₁ and the mass of fluid flowing through section B per second = v₂α₂ρ₂
For streamline flow, the fluid enters through section A and leaves through section B, and does not remain stored in the region between A and B, hence
v₁α₁ρ₁ = v₂α₂ρ₂ ……. (1)
The product vαρ is the mass flow rate. If the fluid is incompressible (like a liquid), then its density is constant and in that case ρ₁ = ρ₂.
∴ v₁α₁ = v₂α₂ ……. (2)
or, vα = constant ……… (3)
Equations (2) and (3) are known as the equations of continuity of liquid flow.
∴ v ∝ \(\frac{1}{\alpha}\), which means that the velocity of liquid flow through any cross section of a tube is inversely proportional to its cross sectional area.
The equations of continuity essentially express the law of conservation of mass.

Energy of Liquid in Streamline Flow

At any point inside a flowing liquid, there are three forms of energy-

1. kinetic energy,
2. potential energy and
3. energy due to pressure.

1. Kinetic energy: If mass m of a liquid flows with a velocity v, then the kinetic energy of that liquid = \(\frac{1}{2}\)mv²
Kinetic energy per unit mass = \(\frac{1}{2}\)v².
Kinetic energy per unit volume
= \(\frac{1}{2} \frac{m}{V} v^2\) [V = volume of the liquid]
= \(\frac{1}{2} \rho \nu^2\) [ρ = \(\frac{m}{V}\) = density of the liquid]

2. Potential energy: If mass m of a liquid is at a height h above the surface of the earth, then the potential energy of that liquid = mgh.
Potential energy per unit mass = gh
Potential energy per unit volume = \(\frac{m g h}{V}\) = ρgh.

3. Energy due to pressure: if a liquid is under the action of some applied pressure, then it acquires some energy and this energy is known as energy due to pressure. The liquid can perform work by expending this energy. Let

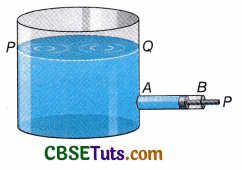
some liquid of density ρ whose free surface is PQ be kept in a container [Fig.]. A narrow side tube AB of cross sectional area a is attached near the bottom of the container. This tube is fitted with a piston P, which can move freely along the tube. If the pressure of the liquid at rest along the axis of the narrow tube is p, then the force acting on the piston = pα. If the piston is slowly pushed inside the tube through a distance x, then work done = pαx. As a result, liquid of volume αx or mass axα enters the container. Since the piston is moved slowly, the liquid acquires negligible velocity and hence it will possess no kinetic energy. So the work done pαx remains stored as potential energy in mass αxp of the liquid that has entered the container. This energy is called the energy due to pressure for the liquid.
The energy due to pressure per unit mass of the liquid = \(\frac{p \alpha x}{\alpha x \rho}\) = \(\frac{p}{\rho}\)
∴ The energy due to pressure per unit volume of the liquid
= \(\frac{p \alpha x}{\alpha x}\) = p