Understanding Physics Topics is essential for solving complex problems in many fields, including engineering and medicine.
Is Poisson’s Ratio an Elastic Modulus?
Under the influence of an external force, when a body elongates in any direction, it also undergoes contraction in a perpendicular direction. Conversely, when a body contracts in any direction under the influence of an external force, it also elongates at the same time in perpendicular directions. So, longitudinal strain and lateral strain occur simultaneously in a body. If the lateral strain is low then it is proportional to its longitudinal strain. The ratio of lateral strain to longitudinal strain is called the Poisson’s ratio.
Poisson’s ratio (σ) \(=\frac{\text { lateral strain }}{\text { longitudinal strain }}\)
Let us consider a wire of initial length L and initial diameter D. If the increase in the length of the wire under the influence of the external force is l and the decrease in its diameter is d, then lateral strain = \(\frac{d}{D}\), longitudinal strain = \(\frac{l}{L}\).
∴ Poisson’s Ratio σ = \(\frac{\frac{d}{D}}{\frac{l}{L}}\) = \(\frac{d}{D} \cdot \frac{L}{l}\)
Poisson’s ratio depends only on the nature of the material of a body. It is a pure number and has no unit since it is a ratio between two strains. It is applicable only to solids. In the case of liquids and gases, Poisson’s ratio is meaningless.
Poisson’s ratio is not an elastic modulus because it is not the ratio of stress to strain. It is an elastic constant. limiting values of Poissons ratio: Theoretically, it can be shown that the maximum value of Poisson’s ratio is +\(\frac{1}{2}\) and its minimum value is -1. But Poisson’s ratio becomes negative only when a body undergoes lateral expansion along with its longitudinal expansion. It cannot be realised in practice. For this reason, the practical values of Poisson’s ratio lie between 0 and +\(\frac{1}{2}\).
Poisson’s ratio-when the volume does not change due to elongation: Let l and r be the length and the radius of circular cross section of a wire. Then, the volume of the wire, V = πr2l.
Differentiating both sides, we get,
dV = πr2dl + πl ᐧ 2rdr.
Here, dV = change in volume
dl = change in length, dr = change in radius.
Since the volume remains unchanged, dV = 0.
∴ 0 = πr2dl + π l2r dr or, 0 = π rdl + π 2ldr
or, rdl = -2ldr or, –\(\frac{d r}{r}\) = \(\frac{d l}{2 l}\)
or, –\(\frac{d r / r}{d i / l}\) = \(\frac{1}{2}\) [negative sign indicates that if l increases, then r decreases].
∴ Poisson’s Ratio, σ \(=\frac{\text { lateral strain }}{\text { longitudinal strain }}\) = \(\frac{-d r / r}{d l / l}\) = \(\frac{1}{2}\) = 0.5.
Numerical Examples
Example 1.
An 8 kg mass is suspended from one end of an iron wire of length 2 m and diameter 1 mm. If the Young’s modulus of iron is 2 × 1012 dyn ᐧ cm-2, then what is the increase In length of the wire? [g = 980 cm ᐧ s-2]
Solution:
Young’s modulus, Y = \(\frac{m g L}{\pi r^2 l}\) or, l = \(\frac{m g L}{Y \pi r^2}\)
Here, m = 8kg = 8000 g, g= 980 cm ᐧ s-2,
L = 2 m = 200 cm, r = \(\frac{1}{2}\)mm = 0.05 cm,
Y = 2 × 1012 dyn ᐧ cm-2
∴ l = \(\frac{8000 \times 980 \times 200}{2 \times 10^{12} \times 3.14 \times(0.05)^2}\) = 0.1 cm = 1 mm
Example 2.
The volume of 1 litre of glycerine decreases by 0.42 cm3 on application of a pressure of 20 kg ᐧ cm-2. Calculate the bulk modulus of glycerine.
Solution:
Bulk modulus, K = \(\frac{p V}{v}\)
Here p = 20 kg ᐧ cm-2 = 20 × 1000 × 980 dyn ᐧ cm-2
V = 1 litre = 1000 cm3, v = 0.42 cm3
∴Bulk modulus, K = \(\frac{20 \times 1000 \times 980 \times 1000}{0.42}\)
= 4.67 × 1010 dyn ᐧ cm-2
= 4.67 × 109 N ᐧ m-2
Example 3.
The upper surface of an aluminium cube of side 10 cm is displaced by 0.03 cm with respect to its firmly held lower surface by a tangential force of 7.5 × 1010 dyn. Calculate the modulus of rigidity of aluminium.
Solution:
Modulus of rigidity, n = \(\frac{F}{A \theta}\)
Here, F = 7.5 × 1010 dyn, A = 10 × 10 = 100 cm2
θ = \(\frac{0.03}{10}\) = 0.003
∴ Modulus of rigidity,
n = \(\frac{7.5 \times 10^{10}}{100 \times 0.003}\)
= 2.5 × 1011 dyn ᐧ cm-2
= 2.5 × 1010 N ᐧ m-2
Example 4.
A metallic wire of length 3 m is stretched to produce an elongation of 2 mm. If the diameter of the wire is 1 mm, then find the decrease in its diameter due to this elongation. Poisson’s ratio for the material of the wire is 0.24.
Solution:
Poisson’s ratio, σ = \(\frac{d}{D} \cdot \frac{L}{l}\) or, d = \(\frac{\sigma D l}{L}\)
Here, σ = 0.24, D = 1 mm = 10-3m, L = 3 m,
l = 2 mm = 2 × 10-3 m
∴ d = \(\frac{0.24 \times 10^{-3} \times 2 \times 10^{-3}}{3}\) = 1.67 ×10-7 m
Example 5.
When a body of mass 5kg is hung from a wire of length 1 m and radius 2 mm, the length increases by 0.1 mm. If the Poisson’s ratio is 0.4, what will be the change in the radius of the wire? If the load is reduced to 2kg, how will the radius change?
Solution:
Poisson’s ratio, σ = \(\frac{d}{D} \cdot \frac{L}{l}\)
[where D, L are the initial diameter and the length of the wire and d, l are the changes in the diameter and in the length of the wire respectively]

Example 6.
The change in length of a wire of a circular cross section is found to be 0.01% due to longitudinal stress. If the Poisson’s ratio for the material is 0.2, what is the percentage change in volume? [WBWF 2000]
Solution:
Let the length of the wire be l, its radius be r and volume be V.

Example 7.
A metallic wire of length and diameter 3 m and 0.001 m respectively is stretched by a load of 10 kg. Young’s modulus and Poisson’s ratio of the material of the wire are respectively 20 × 1010 N ᐧ m-2 and 0.26. Calculate the decrease in the diameter of the wire. (g = 9.8 m ᐧ s-2)
Solution:

Example 8.
A wire of length 2 m and diameter 2 cm is suspended vertically with its top end fixed. Its Poisson’s ratio and Young’s modulus are 0.2 and 1.8 × 10 N ᐧ m-2 respectively. What will be its lateral strain if a load of 1000 kg is suspended at its lower end?
Solution:
Young’s modulus, Y = \(\frac{m g}{\pi r^2} \cdot \frac{L}{l}\)
∴ Longitudinal strain,
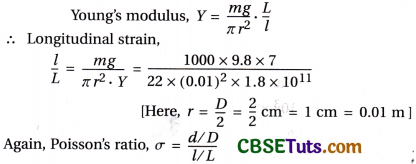

Example 9.
A rubber cord of length 10 m is suspended vertically. How much does it stretch under its own weight? Density of rubber = 1.5 × 103 kg ᐧ m-3; Young’s modulus of rubber = 6 × 106gf ᐧ cm-2; g = 9.8 m ᐧ s-2.
Solution:
Given, L = 10m; ρ = 1.5 × 103 kg ᐧ m-3;
Y = 6 × 106 gf ᐧ cm-2 = 6 × 106 × 980 dyne ᐧ cm-2
= 5.88 × 108 N ᐧ m-2
Let a be the area of cross section of the rubber cord. Then
F = weight of the rubber cord
= L × a × ρ × g
The weight of the rubber cord acts at its centre of gravity and hence the weight of the rubber cord will produce extension in the length [/latex]\frac{L}{2}[/latex] of the cord.
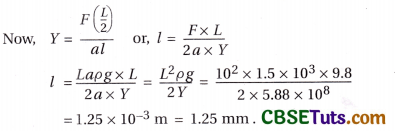
Example 10.
A force of 106 N ᐧ m-2 is required for breaking a material. If the density of the material is 3 × 103 kg ᐧ m-3, then what should be the length of the wire made of this material, so that it breaks due its own weight? [g = 9.8 m ᐧ s-2]
Solution:
Let L be the length of the wire which will break under its own weight. If a is the cross section and ρ is the density of the material of the wire, then,
breaking weight = a × L × ρ × g
= a × L × 3 × 103 × 9.8 = 106 × a
or, L = \(\frac{10^6}{3 \times 10^3 \times 9.8}\) ≈ 34 m