CBSE Sample Papers for Class 12 Physics Paper 6 are part of CBSE Sample Papers for Class 12 Physics. Here we have given CBSE Sample Papers for Class 12 Physics Paper 6
CBSE Sample Papers for Class 12 Physics Paper 6
| Board | CBSE |
| Class | XII |
| Subject | Physics |
| Sample Paper Set | Paper 6 |
| Category | CBSE Sample Papers |
Students who are going to appear for CBSE Class 12 Examinations are advised to practice the CBSE sample papers given here which is designed as per the latest Syllabus and marking scheme as prescribed by the CBSE is given here. Paper 6 of Solved CBSE Sample Paper for Class 12 Physics is given below with free PDF download solutions.
Time Allowed: 3 hours
Maximum Marks: 80
General Instructions
- All questions are compulsory. There are 26 questions in all.
- This question paper has five sections: Section A, Section B, Section C, Section D and Section E.
- Section A contains five questions of 1 mark each. Section B contains five questions of 2 marks each. Section C contains twelve questions of 3 marks each. Section D contains one value based question of 4 marks and Section E contains three questions of 5 marks each.
- There is no overall choice. However, an internal choice has been provided in 1 question of 2 marks, 1 question of 3 marks and all the 3 questions of 5 marks weightage. You have to attempt only 1 of the choices in such questions.
- You may use the following values of physical constants wherever necessary :


Questions
SECTION-A
Question 1.
A compass needle, pivoted about the horizontal axis and free to move in the magnetic meridian, is observed to point along the (i) vertical direction at a point A (ii) horizontal at a place B. Give the value of the angle of dip at these two places.
Question 2.
Give the value of the threshold / knee voltage for a
- silicon diode
- germanium diode
Question 3.
What is the range of frequencies used for TV transmission? What is common between these waves and light wave?
Question 4.
An electron is moving with a velocity v, along the axis of a long straight solenoid, carrying a current I. What will be the force acting on the electron due to the magnetic field of the solenoid?
Question 5. An electrical element X when connected to an alternating voltage source has a current through it leading the voltage by π/2. Identify X and write an expression for its reactance.
SECTION-B
Question 6.
Give the nature of V-I graph for (i) ohmic (ii) non-ohmic circuit elements. Give one example of each type.
Question 7.
Name the phenomenon associated with the production of back emf in a coil due to change of electric current through the coil itself .Name and define the SI unit used for measuring this characteristic of the coil.
Question 8.
Name the device that converts changes in intensity of illumination into changes in electric current. Give any three applications of this device.
OR
A given p-n junction is biased in two different ways as shown in the figure. Identify the type of biasing used in each case. What is the effect of these biasing on the barrier potential across the given p-n junction ?

Question 9.
Find the position of the image formed by the lens of focal length 10 cm shown in the figure. Another lens is placed in contact with this lens to shift the image further away from the lens. What is the nature of the second lens?

Question 10.
Calculate the ratio of de-Broglie wavelengths associated with a deuteron moving with velocity 2v and an alpha particle moving with a velocity v.
SECTION-C
Question 11.
State the two Kirchhoffs rules used to find the current in different branches of the following circuit. Use these rules to write the expressions for the currents I1, I2 and I3 in the circuit diagram shown.

Question 12.
The output of an unregulated dc power supply needs to the regulated. Name the device and its working that can be used for this purpose and draw the relevant circuit diagram.
Question 13.
Figure shows a ray of light passing through a prism. If the refracted ray QR is parallel to the base BC, show that
(i) r1 = r2 = A/2,
(ii) angle of minimum deviation, δm =2i – A

OR
Use Huygens principle to explain the formation of diffraction pattern due to a single slit illuminated by a monochromatic source of light. When the width of the slit is made double the original width, how would this affect the size and intensity of the central diffraction band?
Question 14.
Define the terms (i) disintegration constant and (ii) half-life for a radioactive nucleus. Obtain the relation between the two.
Question 15.
State any three reasons for preferring lasers diode as light sources for optical communication links.
Question 16.
An electric dipole with moment p, is placed in a uniform electric field of intensity \(\vec { E } \) . Write the expression for the torque \(\vec { \tau } \) experienced by the dipole. Identify two pairs of perpendicular vectors in the expression. Show diagrammatically the orientation of the dipole in the field for which the torque is
- Zero
- maximum value
- half the maximum value
Question 17.
State Gauss’s law in electrostatics. Using this law, derive an expression for the electric field due to a uniformly charged infinite plane sheet.
Question 18.
Obtain an expression for the magnetic moment of an electron, moving with a speed ‘V’, in a circular orbit of radius ‘r’. State the rule to find its direction. How does this magnetic moment change when
- the frequency of revolution is doubled
- the orbital radius is halved ?
Question 19.
Electromagnetic waves with wavelength
- λ1 are used to treat muscular strain.
- λ2 are used by a FM radio station for broadcasting.
- λ3 are use to detect fracture in bones.
- λ4 are absorbed by the ozone layer of the atmosphere.
Identify and name the part of electromagnetic spectrum to which these radiations belong. Arrange these wavelengths in decreasing order of magnitude.
Question 20.
Define mass number (A) of an atomic nucleus. Assuming the nucleus to be spherical, give the relation between the mass number (A) and the radius (R) of the nucleus. Calculate the density of nuclear matter. Radius of nucleus of 1H1 =1.1 x 10-15 m.
What is the ratio of the order of magnitude of density of nuclear matter and density of ordinary matter?
Question 21.
For the transistor circuit shown here, identify the
- type of transistor used and
- biasing configuration employed
OR
The output characteristics of the transistors, for this biasing configuration are as shown.

Use this graph to estimate the value of the current amplification factor for the transistor for VCE = 3V.

Question 22.
A ground receiver station is receiving a signal at (a) 5 MHz and (b) 100 MHz, transmitted from a ground transmitter at a height of 300 m. located at a distance of 100 km from the receiver station. Identify whether the signal is coming via space wave propagation or sky wave propagation or via satellite transponder. Radius of earth = 6.4 x 106 m. Nmax of Ionosphere = 1012 m3.
SECTION-D
Question 23.
Ajit had a mobile tower erected on his house. His one neighbour kept complaining to the municipal authorities to remove it as per his thinking it may be a health hazard for his family. Ajit explained him the need for erecting the mobile towers in residential area for efficient transmission of mobile signal with scientific proof that a radiation from a mobile tower in India is within limit and is not a health hazard.
- What values are exhibited by Ajit ?
- What is the nature of the radiation emitted by a mobile tower?
SECTION-E
Question 24.
(a) Explain the capacitance of a parallel plate capacitor with a dielectric slab.
(b) A capacitor of unknown capacitance is connected across a battery of V volts. The charge stored in it is 300 μC. When potential across the capacitor is reduced by 100 V, the charge stored in it becomes 100 μC. Calculate the potential V and the unknown capacitance. What will be the charge stored in the capacitor if the voltage applied had increased by 100 V?
OR
(a) Establish a relation between current and drift velocity.
(b) In a meter bridge, the null point is found at a distance of 40 cm from A. If a resistance of 12Ω is connected in parallel with S, the null point occurs at 50.0 cm from A. Determine the values of R and S.

Question 25.
State Ampere’s circuital theorem and apply it to find the magnetic field inside a (i) solenoid (ii) toroid
OR
Derive an expression for the torque on a current carrying loop kept in a uniform magnetic field.
Question 26.
(a) Define critical angle and total internal reflection. Give the two necessary conditions for total internal reflection.
(b) The image obtained with a convex lens is erect and its length is four times the length of the object. If the focal length of the lens is 20 cm, calculate the object and image distances.
OR
(a) Derive the expression for refraction from convex spherical surface for a real image.
(b) A bi-convex lens has a focal length 2/3 times the radius of curvature of either surface. Calculate the refractive index of lens material.
Answers
SECTION-A
Answer 1.
- Angle of dip at A is 90°
- Angle of dip at B is 0°.
Answer 2.
- Knee voltage for silicon 0.7V
- Knee voltage for germanium 0.2V.
Answer 3.
Range of frequencies used for TV transmission is 54-72 MHz (VHF-Very High Frequencies). Radio waves, visible light and X-rays are transverse waves. These rays are categorized as electromagnetic waves. These waves consist of two fields including magnetic field and electric fields. Electric and magnetic fields are perpendicular to each other but also perpendicular to the direction of propagation of wave. Moreover, light waves, radio waves and X-rays transfer energy from one point to other point, (any one)
Answer 4.
Force is zero because electric V and magnetic field B both are in the same parallel.
Answer 5.
As current through X leads the voltage by y therefore it is a capacitor Xc = \(\frac { 1 }{ \omega C } \) .
SECTION-B
Answer 6.
- The V-I graph for an ohmic material is straight line passing through the origin, e.g., resistor made of manganin.
- V-I graph for non-ohmic material is a curve, i.e. non – linear or straight line not passing through origin e.g., junction diode or electrolyte

Answer 7.
Self induction Henry: Self inductance is defined as the induction of a voltage in a current-carrying wire when the current in the wire itself is changing. In the case of self-inductance, the magnetic field created by a changing current in the circuit itself induces a voltage in the same circuit. Therefore, the voltage is self-induced. Magnitude of emf
e = – L \(\frac { dI }{ dt } \) Or L= – \(\frac { e }{ \frac { dI }{ dt } } \)
Where
e = the induced voltage in volts
L = the value of inductance in Henry
\(\frac { dI }{ dt } \) = the rate of change of current in amperes per second
Putting the following values in the above equations as e =1 V, and \(\frac { dI }{ dt } \) = 1 A/s then the value
of Inductance will be L = 1 H. Hence, from the above derivation, the unit of L can be defined as “a coil is said to have an inductance of 1 Henry if an emf of 1 volts is induced in it when the current flowing through it changes at the rate of 1 Amp/sec”.
Answer 8.
Photocell
Three applications:
(i) Light meters in photographic camera
(ii) Automatic switching on and off of streetlight
(iii) Automatic counting devices
OR
(a) Forward bias
(b) Reverse bias
In forward bias; barrier potential decreases In reverse bias; barrier potential increases.
Answer 9.

Nature of lens L2 is concave
Answer 10.

SECTION-C
Answer 11.
Kirchhoff’s rules:
(i) First Rule or junction rule: At any junction in an electrical circuit, the sum of currents flowing into that junction is equal to the sum of currents flowing out of that node or equivalently i.e. the algebraic sum of currents in a network of conductors meeting at a point is zero. Recalling that current is a signed (positive or negative) quantity reflecting direction towards or away from a junction, this principle can be stated as ∑ I = 0.
(ii) The sum of all the voltages around a loop is equal to zero.
V1 + V2 + V3 + V4 = 0 or ∑V = 0.
i.e. the directed sum of the electrical potential differences (voltage) around any closed network is zero, or more simply, the sum of the emfs in any closed loop is equivalent to the sum of the potential drops in that loop, or the algebraic sum of the products of the resistances of the conductors and the currents in them in a closed loop is equal to the total emf available in that loop. This law is based on the conservation of energy whereby voltage is defined as the energy per unit charge. The total amount of energy . gained per unit charge must be equal to the amount of energy lost per unit charge, as energy and charge are both conserved.

At junction F, I1 +I2 = I3
For loop ABCFA: – 2 + 1 = 4I1 – 3I2
41, – 3I2 = – 1 …(1)
For loop FCDEF: – 1 + 4 = 3I2 + 2I3
3I2 + 2I3 = 3…(2)
Put I3 = I1 +12 in eqn. (2)
3I2 + 2(I1 +12) = 3
2I1,+ 5I2 = 3…(3)
Solving equation (1) and (3) we get
![]()
Answer 12.
Zener diode: A simple voltage regulator circuit that provides almost constant voltage output when supplied from a variable voltage supply. The resistor Rs limits the current flowing through the zener diode. A Zener Diode or “Breakdown Diode”are basically the same as the standard PN junction diode but they are specially designed to have a low and specified reverse breakdown voltage. The Zener diode behaves just like a normal PN junction when biased in the forward direction. However, unlike a conventional diode that blocks any flow of current through itself when reverse biased, as soon as the reverse voltage reaches a pre-determined value, the zener diode begins to conduct in the reverse direction.
This is because when the reverse voltage applied across the zener diode exceeds the rated voltage of the device a process called Avalanche Breakdown occurs in the semiconductor depletion layer and a current starts to flow through the diode to limit this increase in voltage. The current now flowing through the zener diode increases dramatically to the maximum circuit value (which is usually limited by a series resistor) and once achieved, this reverse saturation current remains fairly constant over a wide range of reverse voltages. The voltage point at which the voltage across the zener diode becomes stable is called the “zener voltage”. (Vz).
This zener breakdown voltage on the I-V curve is almost a vertical straight line.
Zener Diode I-V Characteristics

The Zener Diode is used in its “reverse bias” or reverse breakdown mode. i.e. the diodes anode connects to the negative supply. From the I-V characteristics curve above, we can see that the zener diode has a region in its reverse bias characteristics of almost a constant negative voltage regardless of the value of the current flowing through the diode and remains nearly constant even with large changes in current as long as the zener diodes current remains between the breakdown current IZ(min) and the maximum current rating IZ(max). This ability to control itself can be used to great effect to regulate or stabilise a voltage source against supply or load variations. The fact that the voltage across the diode in the breakdown region is almost constant turns out to be an important characteristic of the zener diode as it can be used in the simplest types of voltage regulator applications.
The function of a regulator is to provide a constant output voltage to a load connected in parallel with it in spite of the ripples in the supply voltage or the variation in the load current and the zener diode will continue to regulate the voltage until the diodes current falls below the minimum Iz (min) value in the reverse breakdown region
Answer 13.
In the figure the ray emerges along RS.
If line PQ and SR are produced, they meet at point O as in the figure.
PQ = incident ray
QR = refracted ray and
RS = emergent ray
∠i = angle of incidence at the first face
∠r1 = angle of refraction at first face
∠r2 = angle of incidence at second face
∠e = angle of emergence at the second face.
According to angle of deviation the angle
∠EOR = ∠δ is the angle of deviation due to the
prism. In the figure, we have

OR
Consider a parallel beam of monochromatic light is incident normally in a slit of width b as shown in figure. According to Huygens principle every point of slit acts as a source of secondary wavelets spreading in all directions. Screen is placed at a larger distance. Consider a particular point P on the screen receives waves from all the secondary sources. All these waves start from different point of the slit and interference at point P to give resultant intensity is obtained.

Point P0 is a bisector plane of the slit. At P0, all waves are travelling equal optical path. So all wavelets are in phase thus interface constructively with each other and maximum intensity is observed. As we move from P0, the wave arrives with different phases and intensity is changed. Intensity at point P is given by
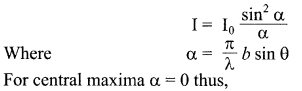
Where a = b sin 0
For central maxima a = 0 thus,
When the width of slitis made double the original width intensity will get four times of its original value.
Width of central maximum is given by,
b = \(\frac { 2D\lambda }{ b } \)
Where, D = Distance between screen and slit,
X = Wavelength of the light, b = size of slit
So with the increase in size of slit the width of central maxima decrease. Hence, double the size of the slit would result in half the width of the central maxima.
Answer 14.
Decay constant, proportionality between the size of a population of radioactive atoms and the rate at which the population decreases because of radioactive decay. Suppose N is the size of a population of radioactive atoms at a given time t, and dN is the amount by which the population decreases in time dt; then the rate of change is given by the equation dN/dt = -λN, where λ is the decay constant. Integration of this equation yields N = N0e-λt, where N0 is the is size of an initial population of radioactive atoms at time t =0. This shows that the population decays exponentially at a rate that depends on the decay constant.
Half-life, in radioactivity, the interval of time required for one-half of the atomic nuclei of a radioactive sample to decay (change spontaneously into other nuclear species by emitting particles and energy), or, equivalently, the time interval required for the number of disintegrations per second of a radioactive material to decrease by one-half. i.e. the time required for half of the original population of radioactive atoms to decay is called the half-life. The relationship between the half-life, T1/2, and the decay constant is given by T1/2 = 0.693/λ.
Answer 15.
Three reasons
- Characteristics compatible with optical fibre
- Gives adequate power
- Give light that can be easily modulated
Answer 16.

Answer 17.
Gauss’s law: The net electric flux through any closed surface is equal to l/ε0 times the net electric charge enclosed within that closed surface.
Gauss’s law may be expressed as:
ΦE=Q/ε0
Where ΦE is the electric flux through a closed surface S enclosing any volume V, Q is the total charge enclosed within S, and ε0 is the electric constant. Electric Field due to A Uniformly Charged Infinite Plane Sheet: Suppose a thin non-conducting infinite sheet of uniform surface charge density σ.

Let Pbe any point at a distance r from the sheet. Let the small area element \(\vec { ds } \)= ds n̂. \(\vec { E } \) and n̂ are perpendicular, on the surface of imagined cylinder, so electric flux is zero. E and h are parallel on the two cylindrical edges P and P’, which contributes electric flux.
Electric charge ovei the edges P and P’ of the cylinder is

Electric field intensity E on either side of the sheet must be perpendicular to the plane of sheet having same magnitude at all points equidistant from sheet

Where n̂ is a unit vector normal to the plane and going away from it.
When σ < 0, E is directed away from both sides. However electric field intensity is independent of r.
Answer 18.
Magnetic moment m = IA = \(\frac { { { er }^{ 2 } }\omega }{ 2 } \) A loop of electric current, a bar magnet, an electron, a molecule, and a planet all have magnetic moments. The magnetic moment may be considered to be a vector having a magnitude and direction. The direction of the magnetic moment points from the south to north pole of the magnet.

- If frequency v = \(\frac { \omega }{ 2\pi } \) is doubled then from the equation magnetic moment would be doubled.
- when orbital radius becomes halved then magnetic moment becomes one fourth.
Answer 19.
- λ1 infra-red
- λ2 radio-waves
- λ3 X-rays
- λ4 ultra-violet rays
λ2 > λ1 > λ4 > λ3
Answer 20.
The mass number (symbol A), also called atomic mass number or nucleon number, is the total number of protons and neutrons (together known as nucleons) in an atomic nucleus. It determines the atomic mass of atoms. The mass number is different for each different isotope of a chemical element. The radius of a nucleus, R, is related to its nucleon number, A, by the equation:

Thus nuclear matter is 10 4 times denser than ordinary matter.
Answer 21.
- n-p-n transistor
- common-emitter configuration
- IB= (60- 10) = 50 mA
Ic= (9.5-2.5) = 7.0 mA
Current amplification factor = Ic/IB =0.14
Answer 22.
Maximum distance covered by space wave communication 2Rh = 62 km.
Critical frequency =ƒc = 9 (Nmax)1/2 \(\simeq \) 9 MHz
- 5 MHz <ƒc ; sky wave propagation (ionospheric propagation)
- 100 MHz > ƒc via satellite transponder
Answer 23.
(1) Caring, convincing, scientific knowledge
(2) Cell phones communicate with nearby cell towers mainly through radio frequency (RF) waves, a form of energy in the electromagnetic spectrum between FM radio waves and microwaves. Like FM radio waves, microwaves, visible light, and heat, are forms of nonionizing radiation, this means they do not directly damage the DNA inside cells. Stronger (ionizing) types of radiation such as X-rays, gamma rays, and ultraviolet (UV) light are thought to be able to cause cancer.
Answer 24.
Let us take a parallel plate capacitor. Suppose the separation distance between the plates is Use air or vacuum as a medium for this experiment. Suppose +Q is the charge on one plate and -Q is charge on the second plate. Bring a rectangular slab made up of conducting material between the plates of the capacitor. The thickness of the slab must be less than the distance between the plates of the capacitor. When the electric field will be applied then polarization of molecules will be started. The polarization will take place in the direction same as that of electric field. Consider a vector that must be polarized, name it as P. The polarization vector must be in the direction of electric field E0. Then this vector will start its functioning and will produce an electric field Ep in the opposite direction to that of E0. The net electric field in the capacitor is shown by the figure.
E = E0 – Ep
The electric field E0 in the outside region of the dielectric will be null. Now the equation of the potential difference between the plates will be:


OR
Therefore, the volume of the conductor = Al
If n is the number of free electrons per unit volume of the conductor, then the total number of free electrons in the conductor = A.l.n. If e is the charge on each electron then total charge on all the free electrons in the conductor
Q=A .l.n.e …(1)
Let a constant potential differences V is applied across the ends of the conductor with the help of a battery
The electric field set up across the conductor is given by
E =V/l …(2)
Due to this field, the free electrons present in the conductor will begin to move with a drift velocity vd towards the left hand side of the conductor.
Thus the time taken by the free electrons to cross the conductor is

Hence the current flowing through a conductor is directly proportional to the drift velocity.

When resistance R and S are connected then balance point is found at a distance 40 cm from the zero

When a resistance 12 Ω is connected in parallel with S then total resistance in the right hand gap is

Answer 25.
Magnetic field of a solenoid

A solenoid is a long wire wound in a close-packed helix carrying a current I and the length of the solenoid is much greater than its diameter Figure here shows a section of a stretched out solenoid in xy and yz plane The solenoid magnetic field is the vector sum of the field produced by the individual turns that make up the solenoid Magnetic field B is nearly uniform and parallel to the axis of the solenoid at interior points near its centre and external field near the centre is very small Consider a dashed closed path abed as shown in figure. Let l be the length of side ab of the loop which is parallel to the axis of the solenoid Let us also consider that sides be and da of the loop are very-very long so that side cd is very much far away from the solenoid and magnetic field at this side is negligibly small and for simplicity we consider it equal to 0 At side ab magnetic field B is approximately parallel and constant. So for this side.
![]()
Magnetic field B is perpendicular to sides be and da, hence these portions of the loop does not make any contributions to the line integral as B.dl = 0 for the side be and da Side cd lies at external points solenoid where B.dl = 0 as B = 0 or negligibly small outside the solenoid Hence sum around the entire closed path reduces to Bl If N are number of turns per unit length in a solenoid then number of turns in length l is nl. The total current through the rectangle abed is NIl and from ampere’s law

we have obtained this relation for infinitely long solenoids considering the field at external points of the solenoid equal to zero. However for real solenoids external field is relatively weak rather then equal to zero Thus for actual solenoids relation (1) holds for internal points near the centre of the solenoid Field at internal points of the solenoid does not depend on length and diameter of the solenoid and is uniform over the cross-section of a solenoid.
Megnetic Field of a toroid:
We will now apply Ampere circuital law to calculate magnetic field of a toroid

A toroidal solenoid is a hollow circular ring with a large number of turns of a wire carrying current wound around the ring. Suppose we have to find the magnetic field B at a point P inside the toroid as shown in figure. In this case Amperion loop would be a circle through point P and Fig- Toroidal solenoid concentric inside the toroid by symmetry field will have equal magnitude at all points of this circle and this field is tangential to every point in the circle

If there are total N number of turns, net current crossing the area bounded by the circle is NI where I is current in the toroid using

Thus we see that field B varies with r i.e. field B is not uniform over the cross-section of the core because the path l = 2πr is longer at the outer side of the section than at the inner side. Imagine a concentric circle through point P outside the toroid.
The net current passing through this circular disc is zero, since the current NI passes in and same current passes out. Thus using Ampere’s circuital law, the field B = 0 outside the toroid.
OR
Consider a rcctangular loop carrying a current i in the B presence of a uniform magnetic field directed parallel to the plane, as shown in Figure. No magnetic forces act on sides I and 3 bccause these wires are parallel to the field; hence, L x B = 0 for these sides. the field. The magnitude of these forces is.
F2 = F4= I ∝ B

The direction of 2, force exerted on wire 2 is out of the page in the view shown in Figure, and that of 4, the force excited on wire 4, is into the page in the same view. If we see the loop from side 3 and sight along side 2 and 4. WC 5CC the view shown in Figure. and thc Iwo forces F2 and F4 are directed as shown. Note that the two forces point in opposite directions but are not directed along the same line of action. If the loop is pivoted so that it can rotate about point O, these two forces produce about O a torque that rotates the ioop clockwise. The magnitude of this torque r max. where the moment arm about O is b/2 for force. Because the area enclosed by the loop is A = ab, we can express the maximum torque as
τ = IAB
if the coil has N turns then total torque is t NIAB.
Answer 26.
Critical Angle:
Critical angle is defined as the angle of incidence that provides an angle of refraction of 90-degrees. The value of the critical angle is dependent upon the combination of materials present on each side of the boundary. For the water-air boundary, the critical angle is 48.6-degrees. For the crown glass-water boundary, the critical angle is 61.0-degrees.
Let’s consider two different media – medium i (incident medium) and medium r (refractive medium). The critical angle is the 0. that gives a Θ value of 90-degrees. If this information is substituted into Snell’s Law equation, a generic equation for predicting the critical angle can be derived.

The critical angle can be calculated by taking the inverse-sine of the ratio of the indices of refraction. As the angle of incidence is increased, the angle of refraction would eventually reach a 90-degree angle. These principles are depicted in the diagram below.

…the refracted ray becomes dimmer (there is less refraction)
…the refracted ray becomes brighter (there is less refraction)
…the angle of refraction aproaches 90 degrees until finally a refracted ray can no longer be seen.
Total internal reflection:
The maximum possible angle for refraction is 90-degrees. If incident angle in the denser medium is greater than critical angle then the ray will not go under refraction. Now all of the energy (the total energy) carried by the incident wave to the boundary stays within the water (internal to the original medium) and undergoes reflection of the boundary. When this happens, total internal reflection (TIR) occurs.
Two Requirements for Total Internal Reflection:
Total internal reflection (TIR) is the phenomenon that involves the reflection of all the incident light of the boundary. TIR only takes place when both of the following two conditions are satisfied:
- the light travels from the more dense medium to the less dense medium.
- the angle of incidence is greater than the critical angle.

Total internal reflection will not take place unless the incident light is traveling within the more optically dense medium towards the less optically dense medium. TIR will happen for light traveling from water towards air, but it will not happen for light traveling from air towards water. The only way for the angle of refraction to be greater than the angle of incidence is for light to bend away from the normal. Since light only bends away from the normal when passing from a more dense medium into a less dense medium, then this would be a necessary condition for total internal reflection.

The source is located at S, and the image will be located at I. The centre of curvature is at O, and the radius of curvature is R. Let the incident ray SA makes an angle x, the refracted ray AI makes an angle z and AO makes an angle y with the optical axis (principal axis).θ1 and θ2 are the incident and refracted angles. The angle x can presumably be measured, and the angles of incidence and refraction are related using our small angle approximation of Snell’s Law. Using the angle sum theorems for lines and triangles, and radian measure, we find that

Using radians, the arc length AB = Ry. For small angles, AB = sx = iz holds. Substituting these formulas into our Snellian approximation gives

In fact, the equation holds for concave boundaries as well, provided we use sign conventions for our measurements s, i, R.

We hope the CBSE Sample Papers for Class 12 Physics Paper 6 help you. If you have any query regarding CBSE Sample Papers for Class 12 Physics Paper 6, drop a comment below and we will get back to you at the earliest.