NCERT Solutions for Class 12 Maths Chapter 6 Application of Derivatives Ex 6.3

NCERT Solutions for Class 12 Maths Chapter 6 Application of Derivatives Ex 6.3 are part of NCERT Solutions for Class 12 Maths. Here we have given NCERT Solutions for Class 12 Maths Chapter 6 Application of Derivatives Ex 6.3.

• Application of Derivatives Class 12 Ex 6.1
• Application of Derivatives Class 12 Ex 6.2
• Application of Derivatives Class 12 Ex 6.4
• Application of Derivatives Class 12 Ex 6.5

Board	CBSE
Textbook	NCERT
Class	Class 12
Subject	Maths
Chapter	Chapter 6
Chapter Name	Application of Derivatives
Exercise	Ex 6.3
Number of Questions Solved	27
Category	NCERT Solutions

NCERT Solutions for Class 12 Maths Chapter 6 Application of Derivatives Ex 6.3

Ex 6.3 Class 12 Maths Question 1.
Find the slope of the tangent to the curve y = 3x⁴ – 4x at x = 4.
Solution:
The curve is y = 3x⁴ – 4x
∴\(\frac { dy }{ dx }\) = 12x³ – 4
∴Req. slope = \({ \left( \frac { dy }{ dx } \right) }_{ x=4 }\)
= 12 x 4³ – 4 = 764.

Ex 6.3 Class 12 Maths Question 2.
Find the slope of the tangent to the curve \(y=\frac { x-1 }{ x-2 } ,x\neq 2\) at x = 10.
Solution:
The curve is \(y=\frac { x-1 }{ x-2 } \)

Ex 6.3 Class 12 Maths Question 3.
Find the slope of the tangent to curve y = x³ – x + 1 at the point whose x-coordinate is 2.
Solution:
The curve is y = x³ – x + 1
\(\frac { dy }{ dx }\) = 3x² – 1
∴slope of tangent = \({ \left( \frac { dy }{ dx } \right) }_{ x=2 }\)
= 3 x 2² – 1
= 11

Ex 6.3 Class 12 Maths Question 4.
Find the slope of the tangent to the curve y = x³ – 3x + 2 at the point whose x-coordinate is 3.
Solution:
The curve is y = x³ – 3x + 2
\(\frac { dy }{ dx }\) = 3x² – 3
∴slope of tangent = \({ \left( \frac { dy }{ dx } \right) }_{ x=3 }\)
= 3 x 3² – 3
= 24

Ex 6.3 Class 12 Maths Question 5.
Find the slope of the normal to the curve x = a cos³ θ, y = a sin³ θ at θ = \(\frac { \pi }{ 4 } \) .
Solution:
\(\frac { dx }{ d\theta } =-3a\quad { cos }^{ 2 }\theta sin\theta ,\frac { dy }{ d\theta } =3a\quad { sin }^{ 2 }\theta cos\theta \)

Ex 6.3 Class 12 Maths Question 6.
Find the slope of the normal to the curve x = 1 – a sin θ, y = b cos² θ at θ = \(\frac { \pi }{ 2 } \)
Solution:
\(\frac { dx }{ d\theta } =-a\quad cos\theta \quad \& \quad \frac { dy }{ d\theta } =2b\quad cos\theta (-sin\theta )\)

Ex 6.3 Class 12 Maths Question 7.
Find points at which the tangent to the curve y = x³ – 3x² – 9x + 7 is parallel to the x-axis.
Solution:
Differentiating w.r.t. x; \(\frac { dy }{ dx }\) = 3 (x – 3) (x + 1)
Tangent is parallel to x-axis if the slope of tangent = 0
or \(\frac { dy }{ dx }=0\)
⇒3(x + 3)(x + 1) = 0
⇒x = -1, 3
when x = -1, y = 12 & When x = 3, y = – 20
Hence the tangent to the given curve are parallel to x-axis at the points (-1, -12), (3, -20)

Ex 6.3 Class 12 Maths Question 8.
Find a point on the curve y = (x – 2)² at which the tangent is parallel to the chord joining the points (2,0) and (4,4).
Solution:
The equation of the curve is y = (x – 2)²
Differentiating w.r.t x
\(\frac { dy }{ dx }=2(x-2)\)
The point A and B are (2,0) and (4,4) respectively.

Slope of AB = \(\frac { { y }_{ 2 }-{ y }_{ 1 } }{ { x }_{ 2 }-{ x }_{ 1 } } =\frac { 4-0 }{ 4-2 } =\frac { 4 }{ 2 } \) = 2 …(i)
Slope of the tangent = 2 (x – 2) ….(ii)
from (i) & (ii) 2 (x – 2)=2
∴ x – 2 = 1 or x = 3
when x = 3,y = (3 – 2)² = 1
∴ The tangent is parallel to the chord AB at (3,1)

Ex 6.3 Class 12 Maths Question 9.
Find the point on the curve y = x³ – 11x + 5 at which the tangent is y = x – 11.
Solution:
Here, y = x³ – 11x + 5
⇒ \(\frac { dy }{ dx }\) = 3x² – 11
The slope of tangent line y = x – 11 is 1
∴ 3x² – 11 = 1
⇒ 3x² = 12
⇒ x² = 4, x = ±2
When x = 2, y = – 9 & when x = -2,y = -13
But (-2, -13) does not lie on the curve
∴ y = x – 11 is the tangent at (2, -9)

Ex 6.3 Class 12 Maths Question 10.
Find the equation of all lines having slope -1 that are tangents to the curve \(y=\frac { 1 }{ x-1 }\), x≠1
Solution:
Here
\(y=\frac { 1 }{ x-1 }\)
⇒ \(\frac { dy }{ dx } =\frac { -1 }{ { (x-1) }^{ 2 } } \)

Ex 6.3 Class 12 Maths Question 11.
Find the equation of ail lines having slope 2 which are tangents to the curve \(y=\frac { 1 }{ x-3 }\), x≠3.
Solution:
Here
\(y=\frac { 1 }{ x-3 }\)
\(\frac { dy }{ dx } ={ (-1)(x-3) }^{ -2 }=\frac { -1 }{ { (x-3) }^{ 2 } } \)
∵ slope of tangent = 2
\(\frac { -1 }{ { (x-3) }^{ 2 } } =2\Rightarrow { (x-3) }^{ 2 }=-\frac { 1 }{ 2 } \)
Which is not possible as (x – 3)² > 0
Thus, no tangent to \(y=\frac { 1 }{ x-3 }\) has slope 2.

Ex 6.3 Class 12 Maths Question 12.
Find the equations of all lines having slope 0 which are tangent to the curve \(y=\frac { 1 }{ { x }^{ 2 }-2x+3 } \)
Solution:
Let the tangent at the point (x₁, y₁) to the curve

Ex 6.3 Class 12 Maths Question 13.
Find points on the curve \(\frac { { x }^{ 2 } }{ 9 } +\frac { { y }^{ 2 } }{ 16 } =1\) at which the tangents are
(a) parallel to x-axis
(b) parallel to y-axis
Solution:
The equation of the curve is \(\frac { { x }^{ 2 } }{ 9 } +\frac { { y }^{ 2 } }{ 16 } =1\)…(i)

Ex 6.3 Class 12 Maths Question 14.
Find the equations of the tangent and normal to the given curves at the indicated points:
(i) y = x⁴ – 6x³ + 13x² – 10x + 5 at (0,5)
(ii) y = x⁴ – 6x³ + 13x² – 10x + 5 at (1,3)
(iii) y = x³ at (1, 1)
(iv) y = x² at (0,0)
(v) x = cos t, y = sin t at t = \(\frac { \pi }{ 4 } \)
Solution:
\(\frac { dy }{ dx } ={ 4x }^{ 3 }-18{ x }^{ 2 }+26x-10\)
Putting x = 0, \(\frac { dy }{ dx } \) at (0,5) = – 10

Ex 6.3 Class 12 Maths Question 15.
Find the equation of the tangent line to the curve y = x² – 2x + 7 which is
(a) parallel to the line 2x – y + 9 = 0
(b) perpendicular to the line 5y – 15x = 13.
Solution:
Equation of the curve is y = x² – 2x + 7 …(i)
\(\frac { dy }{ dx } \) = 2x – 2 = 2(x – 1)
(a) Slope of the line 2x – y + 9 = 0 is 2
⇒ Slope of tangent = \(\frac { dy }{ dx } \) = 2(x – 1) = 2

Ex 6.3 Class 12 Maths Question 16.
Show that the tangents to the curve y = 7x³ + 11 at the points where x = 2 and x = – 2 are parallel.
Solution:
Here, y = 7x³ + 11
=> x \(\frac { dy }{ dx }\) = 21 x²
Now m₁ = slope at x = 2 is \({ \left( \frac { dy }{ dx } \right) }_{ x=2 }\) = 21 x 2² = 84
and m₂ = slope at x = -2 is \({ \left( \frac { dy }{ dx } \right) }_{ x=-2 }\) = 21 x (-2)² = 84
Hence, m₁ = m₂ Thus, the tangents to the given curve at the points where x = 2 and x = – 2 are parallel

Ex 6.3 Class 12 Maths Question 17.
Find the points on the curve y = x³ at which the slope of the tangent is equal to the y-coordinate of the point
Solution:
Let P (x₁, y₁) be the required point.
The given curve is: y = x³

Ex 6.3 Class 12 Maths Question 18.
For the curve y = 4x³ – 2x⁵, find all the points at which the tangent passes through the origin.
Solution:
Let (x₁, y₁) be the required point on the given curve y = 4x³ – 2x⁵, then y₁ = 4x₁³ – 2x₁⁵ …(i)

Ex 6.3 Class 12 Maths Question 19.
Find the points on the curve x² + y² – 2x – 3 = 0 at which the tangents are parallel to the x-axis.
Solution:
Here, x² + y² – 2x – 3 = 0
=> \(\frac { dy }{ dx } =\frac { 1-x }{ y } \)
Tangent is parallel to x-axis, if \(\frac { dy }{ dx }=0\) i.e.
if 1 – x = 0
⇒ x = 1
Putting x = 1 in (i)
⇒ y = ±2
Hence, the required points are (1,2), (1, -2) i.e. (1, ±2).

Ex 6.3 Class 12 Maths Question 20.
Find the equation of the normal at the point (am², am³) for the curve ay² = x³.
Solution:
Here, ay² = x³
\(2ay\frac { dy }{ dx } ={ 3x }^{ 2 }\Rightarrow \frac { dy }{ dx } =\frac { { 3x }^{ 2 } }{ 2ay } \)

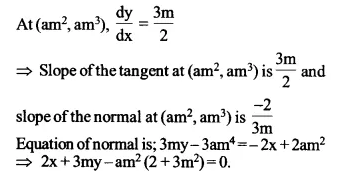
Ex 6.3 Class 12 Maths Question 21.
Find the equation of the normal’s to the curve y = x³ + 2x + 6 which are parallel to the line x + 14y + 4 = 0.
Solution:
Let the required normal be drawn at the point (x₁, y₁)
The equation of the given curve is y = x³ + 2x + 6 …(i)

Ex 6.3 Class 12 Maths Question 22.
Find the equations of the tangent and normal to the parabola y² = 4ax at the point (at²,2at).
Solution:

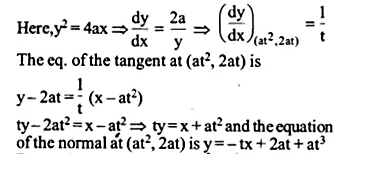
Ex 6.3 Class 12 Maths Question 23.
Prove that the curves x = y² and xy = k cut at right angles if 8k² = 1.
Solution:
The given curves are x = y² …(i)
and xy = k …(ii)

Ex 6.3 Class 12 Maths Question 24.
Find the equations of the tangent and normal to the hyperbola \(\frac { { x }^{ 2 } }{ { a }^{ 2 } } -\frac { { y }^{ 2 } }{ { b }^{ 2 } } =1\) at the point (x₀ ,y₀).
Solution:

Ex 6.3 Class 12 Maths Question 25.
Find the equation of the tangent to the curve \(y=\sqrt { 3x-2 } \) which is parallel to the line 4x – 2y + 5 = 0.
Solution:
Let the point of contact of the tangent line parallel to the given line be P (x₁, y₁) The equation of the curve is \(y=\sqrt { 3x-2 } \)

Choose the correct answer in Exercises 26 and 27.

Ex 6.3 Class 12 Maths Question 26.
The slope of the normal to the curve y = 2x² + 3 sin x at x = 0 is
(a) 3
(b) \(\frac { 1 }{ 3 }\)
(c) -3
(d) \(-\frac { 1 }{ 3 }\)
Solution:
(d) ∵ y = 2x² + 3sinx
∴\(\frac { dy }{ dx }=4x+3cosx\) at
x = 0,\(\frac { dy }{ dx }=3\)
∴ slope = 3
⇒ slope of normal is = \(\frac { 1 }{ 3 }\)

Ex 6.3 Class 12 Maths Question 27.
The line y = x + 1 is a tangent to the curve y² = 4x at the point
(a) (1,2)
(b) (2,1)
(c) (1,-2)
(d) (-1,2)
Solution:
(a) The curve is y² = 4x,
∴ \(\frac { dy }{ dx } =\frac { 4 }{ 2y } =\frac { 2 }{ y } \)
Slope of the given line y = x + 1 is 1 ∴ \(\frac { 2 }{ y }=1\)
y = 2 Putting y= 2 in y² = 4x 2² = 4x
⇒ x = 1
∴ Point of contact is (1,2)

 

We hope the NCERT Solutions for Class 12 Maths Chapter 6 Application of Derivatives Ex 6.3 help you. If you have any query regarding NCERT Solutions for Class 12 Maths Chapter 6 Application of Derivatives Ex 6.3, drop a comment below and we will get back to you at the earliest.