Pair of Linear Equations in Two Variables Class 10 Maths CBSE Important Questions with Solutions

Important Questions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables with solutions includes all the important topics with detailed explanation that aims to help students to score more marks in Board Exams 2020. Students who are preparing for their Class 10 exams must go through Important Questions for Class 10 Math Chapter 3 Pair of Linear Equations in Two Variables.

Important Questions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables

Expert teachers at CBSETuts.com collected and solved 2 Marks and 4 mark important questions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables. All the solutions given in this page are solved based on CBSE marking scheme and NCERT guidelines.

MathsScienceEnglishSocialHindi AHindi B

2016

Short Answer Type Question I [2 Marks]

Question 1.
Solve the following pair of linear equations:
y -4x= 1
6x- 5y= 9
Solution:

Short Answer Type Questions II [3 Marks]

Question 2.
A part of monthly Hostel charge is fixed and the remaining depends on the number of days one has taken food in the mess. When Swati takes food for 20 days, she has to pay 13000 as hostel charges whereas, Mansi who takes food for 25 days pays ? 3500 as hostel charges. Find the fixed charges and the cost of food per day.
Solution:

Question 3.
Solve using cross multiplication method:
x+y=1
2x – 3y = 11
Solution:

Long Answer Type Question [4 Marks]

Question 4.
Draw the graphs of the pair of equations  x + 2y = 5 and 2x-3y = – 4. Also find the points where the lines meet the x-axis.
Solution:

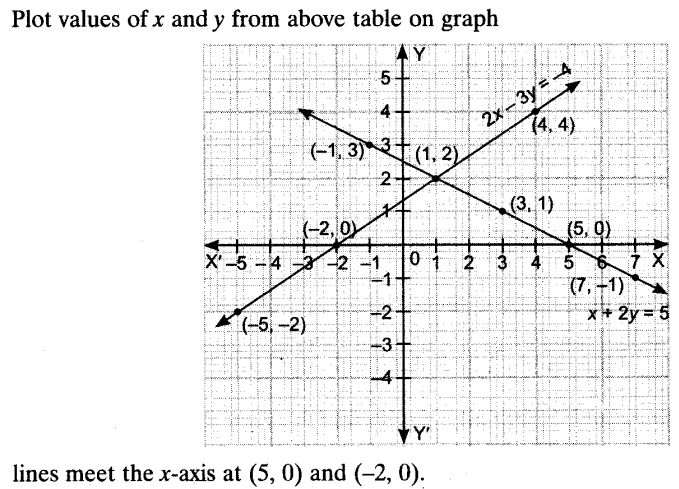
2015

Short Answer Type Question I [2 Marks]

Question 5.
Find whether the lines representing the following pair of linear equations intersect at a point, are parallel or coincident: 2x – 3y + 6 = 0,4x – 5y + 2 = 0
Solution:

Short Answer Type Questions II [3 Marks]

Question 6.
Given a linear equation 3x-5y = 11. Form another linear equation in these variables such that the geometric representation of the pair so formed is:
(i) intersecting lines
(ii) coincident lines
(iii) parallel lines
Solution:

Question 7.
Solve for x and y
x + 2y – 3= 0
3x – 2y + 7 = 0
Solution:

Long Answer Type Question [4 Marks]

Question 8.
4 chairs and 3 tables cost ? 2100 and 5 chairs and 2 tables cost ? 1750. Find the cost of one chair and one table separately
Solution:

2014

Short Answer Type Questions II [3 Marks]

Question 9.
Solve for x andy:
2x= 5y + 4;
3x-2y + 16 = 0
Solution:

Question 10.
Solve for x andy:

Solution:

Question 11.
Solve for x and y:

6(ax + by) = 3a + 2b
6(bx – ay) = 3b -2a

Solution:


Question 12.
Solve the following pair of equations by reducing them to a pair of linear equations:

Solution:

Question 13.
Determine graphically whether the following pair of linear equations 2x – 3y = 5; 3x + 4y = – 1 has
(i) a unique solution
(ii) infinitely many solutions or
(iii) no solution
Solution:

Question 14.
Find those integral values of m for which the c-coordinate of the point of intersection of lines represented by y = mx + 1 and 3x + 4y = 9 is an integer.
Solution:

Long Answer Type Questions [4 Marks]

Question 15.
In a two digit number, the digit in the unit place is twice of the digit in the tenth place. If the digits are reversed, the new number is 27 more than the given number. Find the number.
Solution:

Question 16.
Solve the following system of linear equations graphically.
3x + y – 12 = 0;
x – 3y + 6 = 0
Shade the region bounded by the lines and ii>axis. Also, find the area of shaded region.
Solution:

Question 17.
The owner of a taxi company decides to run all the taxi on CNG fuels instead of petrol/ diesel. The taxi charges in city comprises of fixed charges together with the charge for the distance covered.
For a journey of 13 km, the charge paid is ? 129 and for journey of 22 km, the charge paid is ^ 210.
(i) What will a person have to pay for travelling a distance of 32 km?
(ii) Why did he decide to use CNG for his taxi as a fuel?
Solution:

Question 18.
The area of a rectangle reduces by 160 m if its length is increased by 5 m and breadth is reduced by 4 m. However, if length is decreased by 10 m and breadth is increased by 2 m, then its area is decreased by 100 m2. Find the dimensions of the rectangle.
Solution:

Question 19.
At a certain time in a zoo, the number of heads and the number of legs of tiger and peacocks were counted and it was found that there were 47 heads and 152 legs. Find the number of tigers and peacocks in the zoo:
Why it is necessary to conserve these animals?
Solution:

2013

Short Answer Type Question I [2 Marks]

Question 20.
If the system of equations
6x + 2y = 3 and kx + y = 2 has a unique solution, find the value of k.
Solution:

Short Answer Type Questions II [3 Marks]

Question 21.
Determine the value of m and n so that the following pair of linear equations have infinite number of solutions.
(2m – l)x + 3y = 5;
3x + (n- l)y = 2
Solution:

Question 22.
For what values of p and q will the following pair of linear equations has infinitely many solutions?
4x + 5y = 2;
(2p + 7q)x + (p + 8q)y = 2q-p + 1
Solution:

Question 23.
Solve the following pair of equations for x and y

Solution:

Question 24.
8 men and 12 boys can finish a piece of work in 10 days, while 6 men and 8 boys can finish it in 14 days. Find the time taken by one man alone and that by one boy alone to finish the work.
Solution:

Long Answer Type Questions [4 Marks]

Question 25.
A two digit number is equal to 7 times the sum of its digits. The number formed by reversing its digits is less than the original number by 18. Find the original number.
Solution:

Question 26.
The age of the father is twice the sum of the ages of his 2 children. After 20 years, his age will be equal to the sum of the ages of his children. Find the age of the father.
Solution:

Question 27.
Places A and B are 80 km apart from each other on a highway. A car starts from A and another from B at the same time. If they move in same direction they meet in 8 hrs and if they move in opposite directions they meet in 1 hr 20 minutes. Find speeds of the cars.
Solution:

Long Answer Type Questions [4 Marks]

Question 28.
For what value of k will the pair of equations have no solution?
3x + y = 1
(2k-l)x+ (k-l)y = 2k+l
Solution:

Question 29.
Solve for x and y:

Solution:

Question 30.
Solve the following pair of linear equations graphically, x + 3y = 6;2x-3y = 12
Also find the area of the triangle formed by the lines representing the given equations withy-axis.
Solution:

2011

Short Answer Type Questions I [2 Marks]

Question 31.
Solve: 99x + lOly = 499
lOlx + 99y = 501
Solution:

Question 32.
For what value of p will the following system of equations has no solution;
(2p -1) x + (p -1) y = 2p + 1;
y + 3x – 1 = 0
Solution:

Short Answer Type Questions II [3 Marks]

Question 33.
The sum of the digits of a two digit number is 12. The number obtained by interchanging the two digits exceeds the given number by 18. Find the number.
Solution:

Find the Value of X calculator is a free online tool that gives the value of x when two values are given.

Question 34.
In the figure, ABCDE is a pentagon with BE 11 CD and BC 11 DE. BC is perpendicular to CD. If the perimeter of ABCDE is 21 cm, find the value of x andy.
Solution:


Question 35.
The sum of the numerator and denominator of a fraction is 12. If 1 is added to both the numerator and the denominator the fraction becomes 3/4. Find the fraction.
Solution:

Question 36.
4 men and 6 boys can finish a piece of work in 5 days while 3 men and 4 boys can finish it in 7 days. Find the time taken by 1 man alone or that by 1 boy alone.
Solution:

Question 37.
A man travels 600 km partly by train and partly by car. It takes 8 hours and 40 minutes if he travels 320 km by train and the rest by car. It would take 30 minutes more if he travels 200 km by train and the rest by car. Find the speed of the train and the car separately.
Solution:

Long Answer Type Questions [4 Marks]

Question 38.
Solve the equations graphically:
2x + y = 2;
2y-x = 4
What is the area of the triangle formed by the two lines and the liney = 0?
Solution:

Question 39.
Draw the graphs of the following equations: x + y — 5; x-y = 5
(i) Find the solution of the equations from the graph.
(ii) Shade the triangular region formed by the lines and they-axis.
Solution:

2010

Short Answer Type Questions I [2 Marks]

Question 40.
Find the value of k for which the following pair of linear equations have infinitely
many solutions : 2x + 3y = 7; (k – l)x + (k + 2)y = 3k
Solution:

Question 41.
Find the value of m for which the pair of linear equations 2x + 3y – 7 = 0 and (m – l)x + (m + l)y = (3m – 1) has infinitely many solutions.
Solution:

Question 42.
For what value of k will the following pair of linear equations have no solution?
2x + 3y = 9;
6x + (k – 2)y = (3k – 2).
Solution:

Question 43.
For what value of p will the following pair of linear equations have infinitely many solutions?
(p – 3)x + 3y = p;
px + py = 12
Solution:

Question 44.
Find the values of a and b for which the following pair of linear equations has infinitely many solutions: 2x + 3y = 7; 3/4(a + b)x + (2a – b)y = 21
Solution:

Question 45.
Solve the following pair of equations:

Solution:


Question 46.
The sum of the numerator and the denominator of a fraction is 4 more than twice the numerator. If 3 is added to each of the numerator and denominator, their ratio becomes 2 : 3. Find the fraction. [All India]
Solution:

Question 47.
A number consists of two digits. When the number is divided by the sum of its digits, the quotient is 7. If 27 is subtracted from the number, the digits interchange their places, find the number
Solution:

2009

Very Short Answer Type Questions [1 Mark]

Question 48.
Find the value of a so that the point (3, a), lies on the line represented by 2x-3y = 5
Solution:

Question 49.
Find the number of solutions of the following pair of linear equations .
x + 2y – 8 = 0
2x + 4y = 16
Solution:

Question 50.
Write whether the following pair of linear equations is consistent or not
x +y = 14,
x-y = 4
Solution:

Short Answer Type Questions I [2 Marks]

Question 51.
Find the value of k for which the pair of linear equations
kx + 3y = k – 2 and 12x + ky = k has no solution.
Solution:

Question 52.
Solve for x andy:

Solution:

Question 53.
Without drawing the graph, find out the lines representing the following pair of linear equations intersect at a point, are parallel or coincident.

Solution:

Question 54.
Solve the following system of equations forx andy

Solution:

Question 55.
Solve the following pair of equations

Solution: