Important Questions for Class 10 Maths Chapter 15 Probability with solutions includes all the important topics with detailed explanation that aims to help students to score more marks in Board Exams 2020. Students who are preparing for their Class 10 exams must go through Important Questions for Class 10 Math Chapter 15 Probability.
Important Questions for Class 10 Maths Chapter 15 Probability
Expert teachers at CBSETuts.com collected and solved 2 Marks and 4 mark important questions for Class 10 Maths Chapter 15 Probability.
MathsScienceEnglishSocialHindi AHindi B
2016
Very Short Answer Type Questions [1 Mark]
Question 1.
Cards marked with number 3,4,5,50 are placed in a box and mixed thoroughly. A card is drawn at random from the box. Find the probability that the selected card bears a perfect square number.
Solution:
Total possible outcomes when one card is drawn = 48
When the number on drawn card is a perfect square, total favourable cases are 4, 9, 16, 25, 36,49, i.e. = 6
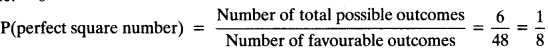
Question 2.
A card is drawn at random from a well shuffled pack of 52 playing cards. Find theprobability of getting neither a red card nor a queen.
Solution:
Number of toal possible outcomes when one card is drawn = 52
Number of favourable outcomes when card is neither red nor queen = 28
![]()
Question 3.
20 tickets, on which numbers 1 to 20 are written, are mixed thoroughly and then a ticket is drawn at random out of them. Find the probability that the number on the drawn ticket is a multiple of 3 or 7.
Solution:
When one ticket is drawn, total possible cases are 20.
Favourable cases when the number is a multiple of 3 or 7 are 3, 6, 9,12,15, 18, 7,14, i.e. 8 cases.
![]()
Short Answer Type Questions II [3 Marks]
Question 4.
In a single throw of a pair of different dice, what is the probability of getting
- a prime number on each dice?
- a total of 9 or 11?
Solution:
Total possible cases when two dice are thrown together = 6 x 6 = 36
Favourable cases when both numbers are prime are (2, 2), (2, 3), (2, 5), (3, 2), (3, 3),(3, 5), (5, 2), (5, 3), (5,5), i.e. 9 outcomes
![]()
(ii) Favourable cases when sum of numbers are 9 or 11 are (3, 6), (4, 5), (5, 4), (5, 6),(6, 3), (6,5), i.e. 6 outcomes
![]()
Question 5.
Two different dice are thrown together. Find the probability of:
- getting a number greater than 3 on each die.
- getting a total of 6 or 7 of the numbers on two dice
Solution:
- When two dice are thrown together total possible outcomes = 6 X 6 = 36
Favourable outcomes when both dice have number more than 3 are (4, 4), (4, 5),(4, 6), (5, 4), (5, 5), (5, 6), (6,4), (6,5), (6, 6), i.e. 9 outcomes.

=9/36=1/4 - Favourable outcomes when sum of the numbers appearing on the dice is 6 or 7 are, i.e. (1,5), (1, 6), (2,4), (2,5), (3,3), (3,4), (4, 2), (4, 3), (5,1), (5,2), (6,1), outcomes.
P(a total of 6 or 7) =11/36
Question 6.
A box consists of 100 shirts of which 88 are good, 8 have minor defects and 4 have major defects. Ramesh, a shopkeeper will buy only those shirts which are good but ‘Kewal’ another shopkeeper will not buy shirts with major defects. A shirt is taken out of the box at random. What is the probability that
- Ramesh will buy the selected shirt?
- ‘Kewal’ will buy the selected shirt?
Solution:
- When one shirt is taken out, then number of total possible outcomes = 100
Ramesh will purchase when shirt is good,
Favourable outcomes = number of good shirts = 88

- Kewal will buy shirt if a shirt is not having major defect.
Number of favourable outcomes = Number of shirts without major defect = 96
P(Kewal buys a shirt) =96/100=24/25
Question 7.
Three different coins are tossed together. Find the probability of getting
- exactly two heads
- at least two heads
- at least two tails.
Solution:
Possible outcomes when three coins are tossed HHH, HHT, HTT, TTT, THH, TTH, HTH, THT
- Number of exactly two heads are HHT, HTH and THH.
P(exactly two heads) = 3/8 - In case of at least two heads, outcomes are HHT, HTH, THH and HHH.
P(at least two heads) = 4/8=1/2 - In case of at least two tails, outcomes are TTH, THT, HTT and TTT.
P(at least two tails) = 4/8=1/2
Question 8.
From a pack of 52 playing cards, Jacks, Queens and Kings of red colour are removed. From the remaining, a card is drawn at random. Find the probability that drawn card is:
- a black king.
- a card of red colour.
- a card of black colour.
Solution:
Removed red colour cards = 3×2 = 6
Remaining cards = 52 – 6 = 46
- Number of black kings = 2
P(a black king) = 2/46=1/23 - Number of red colour cards = 26
Remaining red colour cards = 26 – 6 = 20
P(a card of red colour) = 20/46=10/23 - Number of black cards = 26
P(a black colour card) =26/46=13/23
Question 9.
There are 100 cards in a bag on which numbers from 1 to 100 are written. A card is taken out from the bag at random. Find the probability that the number on the selected card:
- is divisible by 9 and is a perfect square.
- is a prime number greater than 80.
Solution:
Total possible cases = 100
- Favourable cases when number is a perfect square and is divisible by 9 are 9, 36 and 81.
So, number of favourable cases = 3

- Favourable cases the prime numbers greater than 80 are 83, 89 and 97
So, number of favourable cases = 3
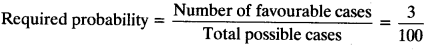
Question 10.
A game consist of tossing a one-rupee coin 3 times and nothing the outcome each time. Ramesh will win the game if all the show the tosses same result, (i.e. either all three heads or all three tails) and loses the game otherwise. Find the probability that Ramesh will lose the game.
Solution:
When three coins are tossed together, then total outcomes are HHH, HHT, HTT, TTT, TTH, THH, HTH, THT Total possible cases = 8
Favourable cases to win the game are HHH or TTT, i.e. two cases.
![]()
Required probability = P(Ramesh will loose the game) = 1 -1/4=3/4
Long Answer Type Questions [4 Marks]
Question 11.
A game of chance consists of spinning an arrow on a circular board, divided into 8 equal parts, which comes to rest pointing at one of the numbers 1,2,3,…, 8 which are equally likely outcomes. What is the probability that the arrow will point at
- an odd number
- a number greater than 3
- a number less than 9.

Solution:
- Total possible outcomes when the arrow points at one of the numbers are 8.
Favourable outcomes when the required number is odd are 1, 3, 5, 7, i.e. 4 outcomes.
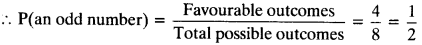
- Favourable outcomes when the required number is more than 3 are 4,5,6,7, 8, i.e. 5 outcomes.

- Favourable outcomes when the required number is less than 9 are 1,2,3,4,5,6,7,8 i.e 8 outcomes
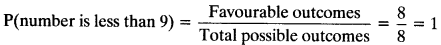
Question 12.
A number JC is selected at random from the numbers 1,2,3 and 4. Another number y is selected at random from the numbers 1, 4, 9 and 16. Find the probability that product of JC and y is less than 16.
Solution:
x can be any one of 1, 2, 3 or 4 andy can be any one of 1, 4, 9 or 16.
Total number of cases of xy = 16
Number of cases when product is less than 16 are 1 x 1,1 x 4,1 x 9, 2 x 1, 2 x 4, 3 x 1, 3 x 4,4 x 1, i.e. 8 cases.
![]()
Question 13.
A number x is selected at random from the numbers 1,4,9,16 and another numbery is selected at random from the numbers 1, 2, 3, 4. Find the probability that the value of xy is more than 16
Solution:
x can be 1, 4, 9 or 16 andy can be 1, 2,3 or 4.
Total number of cases of Ay are 16.
Number of cases when Ay is more than 16 are (9 x 2), (9 x 3), (9 x 4), (16 x 2), (16 x 3), (16 x 4), i.e. 6 cases.
6 3
P(value of xy more than 16) =6/16=3/8
Question 14.
In figure is shown a disc on which a player spins an arrow twice. The fraction a/b is formed, where ‘a’ is the number of sector on which arrow stops on the first and b is the numberof the sector in which the arrow stops on second spin. On each spin, each sector has equal chance of selection by the arrow. Find the probability that the a/b> 1.

Solution:
For a/b > 1, when a = 1, b can not take any value
a = 2, b can take 1 value
a = 3, b can take 2 value, i.e. 1 and 2
a = 4, b can take 3 value, i.e. 1, 2, 3
a = 5, b can take 4 value, i.e. 1, 2, 3,4
a = 6, b can take 5 value, i.e. 1,2,3,4,5
Total possible outcomes = 6 x 6 = 36
Favourable outcomes = 1 + 2 + 3 + 4 + 5 = 15
![]()
2015
Very Short Answer Type Questions [1 Mark]
Question 15.
A letter of english alphabet is chosen at random. Determine the probability that the chosen letter is a consonant.
Solution:
Total english alphabets = 26
Number of consonants in english alphabets = 21
.’. P(Choosing a consonant) =21/26
Question 16.
Two different dice are tossed together. Find the probability that the product of the two numbers on the top of the dice is 6.
Solution:
Total number of possible outcomes = 36
Let A be the event such that
A = Product of the numbers on the top of the dice is 6.
Favourable outcomes (1, 6), (2, 3), (3, 2), (6,1), i.e. 4.
![]()
Question 17.
A game of chance consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8 and these are equally likely outcomes. Find the probability that the arrow will point at any factor of 8.
Solution:
Total outcomes = 8
Factors of 8 are 1, 2, 4 and 8.
Required probability =4/8=1/2
Short Answer Type Questions II [3 Marks]
Question 18.
Two different dice are rolled together. Find the probability of getting:
- the sum of numbers on two dice to be 5.
- even numbers on both dice.
Solution:
Total number of outcomes while rolling two dice = 36.
A: the sum of numbers is 5.
B: even number on both dice.
- Number of favourable cases of event A = 4 [i.e. (1, 4), (4,1), (2,3), (3,2)]
so P(A)=4/36=1/9 - Number of favourable cases of event B = 9 [i.e. (2, 2), (2, 4), (2, 6), (4, 2), (4, 4), (4, 6), (6, 2), (6,4), (6, 6)]
so P(B)=9/36=1/4
Question 19.
Three distinct coins are tossed together. Find the probability of getting:
- at least 2 heads
- at most 2 heads.
Solution:
When three coins are tossed following is the sample space:
{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}
- P(at least 2 heads) =4/8=1/2
- P(at most 2 heads) = 7/8
Question 20.
All red face cards art removed from a pack of playing cards. The remaining cards were well shuffled and then a card is drawn at random from them. Find the probability that the drawn card is
Probability 469
- a red card
- a face card
- a card of club
Solution:
After removing all the red face cards from a pack of playing cards, total number of cards= 52-6 = 46
- P(a red card)=20/46=10/23
- P(a face card)=6/46=3/23
- P(a card of club)=13/46
Question 21.
The probability of selecting a red ball at random from a jar that contains only red, blue and orange balls is 1/4. The probability of selecting a blue ball at random from the same jar is 1/3. If the jar contains 10 orange balls, find the total number of balls in the jar.
Solution:
Let number of red balls in the jar = x
number of blue balls in the jar = y
Total number of balls in the jar = x + y + 10
Probability of selecting red ball =1/4

Question 22.
A bag contains, white, black and red balls only. A ball is drawn at random from the bag. If the probability of getting a white ball is 3/10 and that of a black ball is 2/5,then find the probability of getting a red ball. If the bag contains 20 black balls, then find the total number of balls in the bag.
Solution:
Let R = getting a red ball
B = getting a black ball
W = getting a white ball
Now, P(R) + P(B) + P(W) = 1
P(R)=+ 2/5 + 3/10 = 1
P(R)=1-2/5-3/10=10-4-3/10=3/10
Let total number of balls = x
P(B)=20/x=2/5=20/x
x=20X5/2
Total number of balls = 50
Question 23.
A bag contains 18 balls out of which x balls are red.
- If one ball is drawn at random from the bag, what is the probability that it is not red?
- If 2 more red balls are put in the bag, the probability of drawing a red ball will be 9/8 times the probability of drawing a red ball in the first case. Find the 8
value of X.
Solution:
- Number of non red balls = 18 -x
Probability that ball drawn is not red =18-x/18 - Probability that ball drawn is red=x/18
When 2 more red balls are put in the bag, then number of balls in the bag is 20.
Now, number of red balls = x + 2
Probability that ball drawn is red=x+2/20
According to question,
x+2/20=9/8Xx/18
x + 2 /20= x/16
16x+32=20x
4x=32
x=8
Question 24.
A game consists of tossing a one-rupee coin three times and noting its outcome each time. Find the probability of getting
- three heads.
- at least two tails.
Solution:
Possible outcomes HHH, HHT, HTH, THH, TTT, TTH, THT, HTT
Total number of outcomes = 8
- A = getting three heads, 1 [i.e. HHH]
P(A) =1/8 - B = getting at least two tails, 4[i.e. TTT, TTH, THT, HTT]
P(B)=4/8=1/2
Question 25.
A bag contains 20 balls out of which x balls are red.
- If one ball is drawn at random from the bag, find the probability that it is not red.
- If 4 more red balls are put into the bag, the probability of drawing are red ball will be 5/4 times the probability of drawing a red ball in the first case. Find the value of X.
Solution:
Similar to Ans. 23.
Long Answer Type Questions [4 Marks]
Question 26.
A bag contains 25 cards numbered from 1 to 25. A card is drawn at random from the bag. Find the probability that the number on the drawn card is:
- divisible by 3 or 5.
- a perfect square number.
Solution:
- Number from 1 to 25 which are divisible by 3 or 5 are 3, 6, 9,12,15,18, 21, 24, 5,10,20,25.
P(a number divisible by 3 or 5) = 12/25 - Number from 1 to 25 which are perfect square are 1, 4, 9,16, 25
P(a perfect square number) = ^5/25= 1/5.
Question 27.
A box contains 20 cards numbered from 1 to 20. A card is drawn at random from the box. Find the probability that the number on the drawn card is
- divisible by 2 or 3.
- a prime number.
Solution:
- Numbers from 1 to 20 which are divisible by 2 or 3 are 2,4, 6,8,10,12,14,16,18, 20, 3, 9,15
P(a number divisible by 2 or 3) =13/20 - Prime numbers from 1 to 20 are 2, 3,5, 7,11,13,17,19
P(a prime number) = 8/20=2/5
Question 28.
A card is drawn at random from a well-shuffled deck of playing cards. Find the probability that the card drawn is
- a a card of spade or an ace.
- a black king.
- neither a jack nor a king
- either a king or a queen
Solution:
Total number of outcomes = 52
- A = Card is spade or an ace
Cards favourable to A = 13 + 3 = 16
P(A)=16/52=4/13 - B = Card is black king
Number of black kings = 2
P(B)=2/52=1/26 - C = Card is neither a jack nor a king
Number of favourable cards to C = 52-4-4 = 44
P(C) =44/52=11/13 - D = Card is either a king or a queen
Number of cards favourable to D = 4 + 4 = 8
P(D) = 8/52=2/13
Question 29.
A box contains cards bearing numbers from 6 to 70. If one card is drawn at random from the box, find the probability that it bears
- a one digit number.
- a number divisible by 5.
- an odd number less than 30.
- a composite number between
50 and 70.
Solution:
Number of cards in the box = 65
- Cards bearing one digit number are 6, 7,8, 9 (i.e. 4 cards)
Probability of card bears a one digit number=4/65 - B : Number on the cards is divisible by 5.
Cards favourable to B are 10,15,20,25,30,35,40,45,50,55,60,65,70 (i.e. 13 cards).
P(B)=13/65=1/5 - C: Cards with an odd number less than 30.
Cards favourable to C are 7, 9,11,13,15,17,19, 21,23, 25, 27, 29 (i.e. 12 cards).
P(C)=12/65 - D : Card with composite number between 50 and 70.
Cards favourable to D are 51,52,54,55,56,57,58,60,62,63,64,65, 66,68, 69 (i.e. 15 cards).
P(D) =15/65=3/13
2014
Short Answer Type Questions I [2 Marks]
Question 30.
Rahim tosses two different coins simultaneously. Find the probability of getting at least one tail.
Solution:
Total cases are {HH, HT, TH, TT}.
Favourable cases are (HT, TH, TT}.
.’. Required probability =3/4
Question 31.
Two different dice are tossed together. Find the probability
- that the number on each die is even.
- that the sum of numbers appearing on the two dice is 5
Solution:
Two different dice are tossed. Therefore, total outcomes are 36.
- Favourable outcomes for even number on both dice = 9, [i.e. (2, 2), (2, 4), (2, 6), (4, 2), (4, 4), (4, 6), (6, 2), (6, 4), (6, 6)].
Probability of getting even number on both dice =9/36=1/4 - Favourable outcomes that the sum of the numbers appearing on two dice is 5 are(1,4), (2, 3), (3, 2), (4,1), i.e. 4.
Probability of getting sum of numbers appearing on two dice is 5 = 4/36=1/9
Question 32.
Two different dice are rolled simultaneously. Find the probability that the sum of numbers appearing on the two dice is 10.
Solution:
When two different dice are rolled, then total possible outcomes = 36.
Favourable outcomes for sum of the numbers appearing on two dice is 10 = 3, i.e. {(4, 6), (5, 5), (6, 4)}
Probability of getting the sum of numbers appearing on two dice is 10=3/36=1/12
Long Answer Type Questions [4 Marks]
Question 33.
A bag. contains cards numbered from 1 to 49. A and C is drawn from the beg at random, after mixing the cards thoroughly. Find the probability that the number on the drawn card is
- an odd number.
- a multiple of 5.
- a perfect square.
- an even prime number
Solution:
Total number of cards in a bag = 49.
- Number of odd number cards = 25
.’.Required probability = 25/49 - Number of multiple of 5 = 9 (i.e. 5,10,15, 20, 25, 30, 35,40, 45)
.’.Required probability = 9/49 - Number of perfect square = 7 (i.e. 1,4,9,16, 25, 36,49)
.’. Required probability = 7/49=1/7 - Number of prime number = 1 (i.e. 2)
.’. Required probability = 1/49
Question 34.
All the black face cards are removed from a pack of 52 playing cards. The remaining cards are well shuffled and then a card is drawn at random. Find the probability of getting a
- face C and.
- red card.
- black card.
- king
Solution:
Total cards = 52
Total black face cards = 6
After removing black face cards from a pack of 52 cards, number of remaining cards
= 52-6 = 46.
- Number of face cards in remaining cards = 6 (i.e. 2 red kings, 2 red queens and 2 red jacks)
Required probability =6/46=3/23 - Number of red cards in remaining cards = 26
Required probability =26/46=13/23 - Number of black cards in remaining cards = 20
Required probability=20/46=10/23 - Number of kings in remaining cards = 2 (i.e. 2 red kings)
Required probabilit=2/46=1/23
Question 35.
Cards numbered from 11 to 60 are kept in a box. If a card is drawn at random from the box, find the probability that the number on the drawn card is
- an odd number.
- a perfect square number.
- divisible by 5.
- a prime member less than 20.
Solution:
Total number of cards from 11 to 60 = 50.
- Favourable cases for odd number = 25
.’. Required probability =25/50=1/2 - Number of perfect square numbers from 11 to 60 = 4 (i.e. 16, 25, 36, 49)
.’. Required probability=4/50=2/25 - Number of multiples of 5 = 10 (i.e. 15, 20, 25, 30, 35, 40,45, 50, 55, 60)
.’. Required probability =10/50=1/5 - Number of prime numbers less than 20 = 4 (i.e. 11,13,17,19)
.’. Required probability =4/50=2/25
Question 36.
Red queens and blackjacks are removed from a pack of 52 playing cards. A card is drawn at random from the remaining cards, after reshuffling them. Find the probability that the drawn card is
- a king.
- of red colour.
- a face card.
- a queen.
Solution:
Red queens and blackjacks, i.e. 2 + 2 = 4 cards are removed from a pack of 52 playing cards. Remaining cards = 52 – 4 = 48.
.’. Possible outcomes of drawing one card from 48 cards is 48.
- Favourable outcomes for drawing a king are 4.
.’. Probability of drawing a queen=4/48=1/12 - Favourable outcomes for a card of red colour are 24 as 2 red queens have been removed.
.’. Probability of drawing a queen=24/48=1/2 - Favourable outcomes for a face card (4 kings, 2 queens, 2 jacks) = 8
.’. Probability of drawing a queen=8/48=1/6 - Favourable outcomes for drawing a queen are 2, as 2 red queens have been removed.
.’. Probability of drawing a queen = 2/48=1/24
Question 37.
All the red face cards are removed from a pack of 52 playing cards. A card is drawn at random from the remaining cards, after reshuffling them. Find the probability that the drawn card is
- of red colour.
- a queen.
- an ace.
- a face card.
Solution:
Face cards are taken as (4 jacks, 4 queens and 4 kings):
As all the red face cards are removed
.’. 6 cards (2 jacks, 2 queens and 2 kings) are removed from 52 cards.
.’. Remaining cards = 52 – 6 = 46 cards
.’. Total outcomes of drawing a card from 46 cards = 46
- Favourable outcomes of drawing a red card= 20 (as 6 red cards from 26 have been removed)
.’. Probability of drawing a red card = 20/46=10/23 - Favourable outcomes of drawing a queen= 2 (as 2 red queens have been removed out of 4)
.’. Probability of drawing a queen = 2/46=1/23 - Favourable outcomes of drawing an ace = 4
.’. Probability of drawing an ace = 4/46=2/23 - Favourable outcomes of drawing a face card= 6 (as 2 jacks, 2 queens and 2 kings have been removed)
.’. Probability of drawing a face card=6/46=3/23
Question 38.
Five cards – the ten, jack, queen, king and ace of diamonds, are well shuffled with their faces downwards. One card is then picked up at random.
- What is the probability that the drawn card is the queen?
- If the queen is drawn and put aside, and a second card is drawn, find the probability that the second card is
- an ace
- a queen.
Solution:
Five cards: the ten, jack, queen, king and ace of diamonds are shuffled with faces downwards.
Total possibilities of selecting one card = 5
- Favourable outcomes for drawing a queen = 1
Probability of drawing a queen = 1/5 - When queen is kept aside, then remaining cards = 4
So, total outcomes of drawing a card = 4
- favourable outcomes of drawing an ace is 1
Probability of drawing an ace =1/4 - Favourable outcomes of drawing a queen = 0 (as there is no card of queen).
Probability of drawing a queen=0/4,i.e.0
Question 39.
Cards numbered 1 to 30 are put in a bag. A card is drawn at random from this bag. Find the probability that the number on the drawn card is
- not divisible by 3.
- a prime number greater than 7.
- not a perfect square number
Solution:
Total possible outcomes of drawing a card from a bag out of 30 cards is 30.
- Favourable outcomes for a card numbered not divisible by 3 = 20 (i.e. 1, 2, 4, 5, 7, 8, , 10,11,13,14,16,17,19, 20,22,23,25, 26, 28 and 29).
.’. Probability of drawing a card numbered not divisible by 3 =20/30=2/3 - Favourable outcomes for a prime numbered card greater than 7
= 6 (i.e. 11,13,17,19, 23 and 29)
.’. Probability of drawing a prime numbered card greater than 7 - Favourable outcomes for not a perfect square numbered card
= 25 (leaving 1, 4, 9,16 and 25)
.’. Probability of drawing a card which is not a perfect square =25/30=5/6
Question 40.
A dice is rolled twice. Find the probability that
- 5 will not come up either time
- 5 will come up exactly one time
Solution:
When a die is rolled twice, total possible outcomes = 36.
- Favourable outcomes that 5 will not come either time are 25[(1, 1), (1,2), (1, 3),(1,4), (1,6), (2,1), (2,2), (2,3), (2,4), (2,6), (3,1), (3,2), (3,3), (3,4), (3,6), (4,1), (4,2), (4, 3), (4, 4), (4, 6), (6,1), (6, 2), (6, 3), (6, 4), (6, 6)]
Probability that 5 will not come either time = 25/36 - Favourable outcomes that 5 comes up exactly once are 10[(5,1), (5, 2), (5, 3), (5,4), (5, 6), (1, 5), (2, 5), (3, 5), (4, 5), (6, 5)]
Probability that 5 will come up exactly once = 10/36=5/18
Question 41.
A piggy bank contains hundred 50 p coins, fifty 1 coins, twenty 2 coins and ten 5 coins. If it is equally likely that one of the coins will fall out when the bank is turned upside down, find the probability that the coin which fell
- will be a 50 p coin
- will be of value more than 1
- will be of value less than 5
- will be a 1 or 2 coin
Solution:
Total coins in piggy bank are:
50 p coins = 100; 1 coins = 50; 2 coins = 20; 5 coins = 10
Total coins = 100 + 50 + 20 + 10 = 180
Therefore, total possible outcomes that one coin will fall = 180
- Favourable outcomes for falling a 50 p coin = 100
.’.Probability that a 50 p coin falls =100/180=5/9 - Favourable outcomes for a coin of value more than 1 are 30 (20 + 10).
.’.Probability of falling a coin of value more than 1=30/180=1/6 - Favourable outcomes for falling a coin of value less than ? 5 are 170 (100 + 50 + 20)
.’.Probability of falling a coin of value less than 5 = 170/180=17/18 - Favourable outcomes for falling a coin of value 1 or 2 = 70(50 + 20)
.’. Probability of falling a coin of value 1 or 2 =7/180=7/18
2013
Short Answer Type Questions I [2 Marks]
Question 42.
A card is drawn at random from a well shuffled pack of 52 playing cards. Find the probability that the drawn card is neither a jack nor an ace
Solution:
Total cards = 52
Number of jacks + Number of ace = 4 + 4 = 8
Number of cards neither a jack nor an ace = 52 – 8 = 44
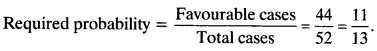
Question 43.
A die is tossed once. Find the probability of getting an even number or a multiple of 3.
Solution:
Even numbers on a die are 2,4, 6.
Multiple of 3 are 3, 6.
So, total favourable cases are 2, 4, 6, 3.
So, required probability =4/6=2/3
Question 44.
A card is drawn at random from a well shuffled pack of 52 playing cards. Find the probability that the drawn card is neither a king nor a queen.
Solution:
Total cards = 52.
Number of kings + number of queen = 4 + 4 = 8
Number of cards neither a king nor a queen = 52 – 8 = 44.
So, required probability =44/52=11/13
Question 45.
Two coins are tossed simultaneously. Find the probability of getting at least one head.
Solution:
Possible outcomes on tossing two coins: HH, HT, TH, TT
Number of total possible outcomes = 4
Favourable outcomes of getting at least one head: HT, TH, HH
Number of favourable outcomes = 3
Required probability=3/4
Question 46.
Three coins are tossed simultaneously. Find the probability of getting Exactly two heads.
Solution:
Possible outcomes when 3 coins are tossed are 8 (i.e. HHH, HHT, HTH, THH, TTH, TTT, THT, HTT).
Favourable cases for exactly 2 heads are 3 (i.e. HHT, HTH, THH)
Required probability = 3/8
Question 47.
Two dice are thrown simultaneously. Find the probability of getting a doublet.
Solution:
Two dice are thrown. So, total number of possible outcomes are 36.
Doublet are (1,1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)
Number of favourable cases = 6
Required probability =6/36=1/6
Question 48.
Three cards of spades are lost from a pack of 52 playing cards. The remaining cards were well shuffled and then a card was drawn at random from them. Find the probability that the drawn card is of black colour.
Solution:
Number of cards left = 52 – 3 = 49
Number of cards of spade left = 13 – 3 = 10
Number of black cards left = 13 + 10 = 23 [ .’. Spade is of black colour]
Total Number of ways to draw a card = 49
Number of ways to draw a black card = 23
Required probability=23/49
Question 49.
The ace, jack, queen and king of clubs are removed from a pack of 52 playing cards. Remaining cards are well shuffled and a card is drawn from them at random. Find the probability that the drawn card is of black colour.
Solution:
Ace, jack, queen, king of clubs are removed from a deck of playing cards.
Number of Remaining cards = 52 – 4 = 48
Number of black cards remain = 22
(jack, ace, queen, king of club are removed).
Required Probability = 22/48=11/24
Question 50.
Out of cards numbered from 1 to 20, which are mixed thoroughly, a card is drawn at random. Find the probability that the drawn card bears a number which is a multiple of 3 or 7.
Solution:
Number of total cards from 1 to 20 = 20
Total possible outcomes = 20
Multiple of 3 or 7 in between 1 to 20 are 3, 6, 9,12,15,18, 7,14
Number of favourable outcomes = 8
Required Probability=8/20=2/25
Long Answer Type Questions [4 Marks]
Question 51.
A group consists of 12 persons, of which 3 are extremely patient, other 6 are extremely honest and rest are extremely kind. A person from the group is selected at random. Assuming that each person is equally likely to be selected, find the probability of selecting a person who is
- extremely patient
- extremely kind or honest.
Which of the above values you prefer more?
Solution:
Total number of persons = 12
Number of extremely patient = 3
Number of extremely honest = 6
Number of extremely kind = 12 -(6+ 3) = 3
- Probability of selecting extremely patient = 3/12=1/4
- Probability of selecting extremely kind or honest = 3+6/12=9/12=3/4
We prefer one should be honest first
Question 52.
A box contains cards numbered 3,5,7,9,…, 35,37. A card is drawn at random from the box. Find the probability that the number on the drawn card is a prime number.
Solution:
Total no. of cards in the box = 18
Number of ways to draw one card = 18
Number of cards with a prime number are 11 (i.e. 3,5, 7,11,13,17,19, 23, 29, 31, 37)
Number of ways to draw a card bearing a prime number = 11
Required probability =11/18
Question 53.
A die is thrown twice. Find the probability that
- 5 may not come either time.
- same number may not come on the die thrown two times.
Solution:
Total outcomes
(1.1),(1,2), (1,3), (1,4),(1,5), (1,6)
(2.1),(2, 2),(2,3),(2,4),(2,5),(2, 6)
(3.1),(3, 2),(3, 3),(3,4),(3,5),(3, 6)
(4.1),(4, 2),(4, 3),(4,4),(4, 5),(4, 6)
(5.1),(5, 2),(5, 3),(5,4),(5, 5),(5, 6)
(6.1),(6,2),(6, 3),(6,4), (6, 5),(6, 6)
Number of total outcome = 36
- Number of outcomes when 5 may not come either time = Outcome except
(1,5), (2,5), (3,5), (4,5), (5,1), (5,2), (5,3), (5,4), (5,5), (5,6), (6,5),= 36 -11 = 25
Probability that 5 may not come either time = 25/36 - Number of outcome when same number may not come on the dice thrown two times = Number of outcomes except (1,1), (2, 2), (3, 3), (4,4), (5, 5), (6, 6) = 36 – 6 = 30
Probability that same number may not come on the dice thrown two times = 30\36=5/6
Question 54.
A bag contains 12 balls, out of which x are white.
- If one ball is drawn at random, find the probability that it is a white ball.
- If 6 more white balls are put in the bag, the probability of drawing a white ball is double than that in
- Find x.
Solution:

Question 55.
Two dice are thrown simultaneously. Determine the probability that the difference of the numbers on the two dice is 2
Solution:
Two dice are thrown
Total possible outcomes = 36
Favourable outcomes, that difference of numbers on the two dice is 2 are.
(1, 3), (3,1), (2, 4), (4,2), (3, 5), (5, 3), (4, 6), (6, 4)
Number of favourable outcomes = 8
Required Probability =8/36=2/9
2012
Short Answer Type Questions I [2 Marks]
Question 56.
A card is drawn at random from a well-shuffled pack of 52 playing cards. Find the probability of getting
- a red king.
- a queen or a jack
Solution:
- Total cards = 52
Number of red kings = 2
Probability (a red king) = 2/52=1/26 - Number of queen=4
Number of jack= 4
Number of favourable cards = 8
P(a queen or a jack)=8/52=2/13
Question 57.

The die is thrown once. Find the probability of getting
- A
- D
Solution:
Total cases = 6
- There are three faces marked with A.
Probability of getting A = 3/6=1/2 - There is one face marked with D.
Probability of getting D =1/6
Question 58.
A box contains 100 red cards, 200 yellow cards and 50 blue cards. If a card is drawn at random from the box, then find the probability that it will be
- a blue card
- not a yellow card
- neither yellow nor a blue card.
Solution:
Red cards = 100; Yellow cards = 200; Blue cards = 50
- P(a blue card) = 50/350=1/7
- P(not a yellow card) = 150/350=3/7
- P(neither yellow nor blue cards) = P(only red card) =100/350=2/7
Short Answer Type Questions II [3 Marks]
Question 59.
A card is drawn from a well shuffled deck of 52 cards. Find the probability of getting
- a king of red colour
- a face card
- the queen of diamonds.
Solution:
Total cards = 52
- P(a king of red colour) =2/52=1/26
- P(a face card)=12/52=3/13
- P(a queen of diamonds)=1/52
Question 60.
A box contains 35 blue, 25 white and 40 red marbles. If a marble is drawn at random from the box, find the probability that the drawn marble is
- white
- no blue
- neither white nor blue.
Solution:
Given: Number of blue marbles = 35; Number of white marbles = 25;
Number of red marbles = 40
Total number of marbles = 100
- P(white marble) =25/100=1/4
- P(no blue marble) = 25+40/100=65/100=13/20
- P(neither white nor blue) = 40/100=2/5
Question 61.
A box contains 70 cards numbered from 1 to 70. If one card is drawn at random from the box, find the probability that it bears
- a perfect square number.
- a number divisible by 2 and 3
Solution:

Question 62.
All kings, queens and aces are removed from a pack of 52 cards. The remaining cards are well shuffled and then a card is drawn from it. Find the probability that the drawn card is
- a black face card.
- a red card
Solution:
Number of kings = 4, number of queens = 4, number of aces = 4
After removing all kings, queens and aces, number of remaining cards = 52 – 12 = 40
- Number of black face cards in the remaining cards (2 jacks) = 2
Probability of black face card = 2/40=1/20 - Out of removed 12 cards, 6 are of red colour.
Number of red coloured cards in remaining cards = 26 – 6 = 20
Probability of getting a red card =20/40=1/2
Question 63.
Card marked with numbers 1, 3, 5, …, 101 are placed in a bag and mixed thoroughly. A card is then drawn at random from the bag. Find the probability that the number on the drawn card is
- less than 19,
- a prime number less than 20.
Solution:
Total number of cards in the bag = 51
- Number of cards bearing a number less than 19 are 9 (i.e. 1, 3, 5, 7, 9,11,13,15,17).
.’. Probability that the number on the drawn card is less than 19 = 9/51=3/17 - Number of cards bearing a prime number less than 20 are 7 (i.e. 3,5, 7,11,13,17,19).
.’.Probability that the number on the drawn card is a prime number less than 20 =7/51
Question 64.
A die is thrown once. Find the probability of getting the following:
- a prime number
- a number lying between 2 and 5.
Solution:
The possible outcomes are = 6 (i.e. 1, 2, 3, 4, 5, 6). .
- Prime numbers on a die = {2, 3, 5}
P(getting a prime number) =3/6=1/2 - Number lying between 2 and 5 are 2 (i.e. 3, 4).
P(getting a number lying between 2 and 5) =2/6=1/3
Question 65.
A box contains 75 cards which are numbered from 1 to 75. If one card is drawn at random from the box, find the probability that the drawn card bears
- a two-digit number.
- a perfect square number
Solution:
Total number of cards = 75
- Total number of two digit numbers from 1 to 75 = 66
P (getting a two digit number) =66/75=22/25 - Perfect square numbers from 1 to 75 are 8 (i.e. 1, 4, 9,16, 25, 36,49, 64).
P(getting a perfect square number) = 8/75
2011
Very Short Answer Type Questions I [2 Marks]
Question 66.
A coin is tossed two times. Find the probability of getting at least one head.
Solution:
Total outcomes are 4, i.e. (HH, HT, TH, TT}
Favourable outcomes are 3, i.e. {HH, HT and TH}
P(at least one head)=3/4
Question 67.
A coin is tossed two times. Find the probability of getting both heads or both tails.
Solution:
Total number of cases while tossing a coin two times are 4, i.e. {HH, HT, TH, TT}
Favourable cases of getting both heads or both tails are 2, i.e. {HH, TT}
![]()
Question 68.
A coin is tossed two times. Find the probability of getting not more than one head.
Solution:
Total number of cases while tossing a coin two times are 4, i.e. (HH, HT, TH, TT}
Favourable cases of getting not more than one head are 3, i.e. {HT, TH, TT}
![]()
Question 69.
A ticket is drawn at random from a bag containing tickets numbered from 1 to 40. Find the probability that the selected ticket has a number which is a multiple of 5.
Solution:
Total number of tickets = 40
Multiples of 5 are 5,10,15,20,25,30,35,40
Number of favourable tickets = 8
.’. P(a number which is a multiple of 5) =8/40=1/5
Question 70.
Two different dice are thrown at the same time. Find the probability that the sum of the two numbers appearing on the top of the dice is 7.
Solution:
Total number of cases while throwing two dice = 36
Number of favourable cases whose sum is 7 are 6, i.e. {1, 6}, (2,5), (3, 4), (4,3), (5, 2), (6,1)
![]()
Short Answer Type Questions II [3 Marks]
Question 71.
A game consists of tossing a coin 3 times and noting its outcome each time. Hanif wins if he gets three heads or three tails, and loses otherwise. Calculate the probability that Hanif will lose the game.
Solution:
Total possible outcomes are 8, i.e. {HHH, TTT, HHT, HTH, HTT, THH, THT, TTH}
There are only two outcomes at which Hanif can win, i.e. {HHH, TTT}, i.e. 2
.’. P(Hanif will lose the game)=6/8=3/4
Question 72.
Two dice are rolled once. Find the probability of getting such numbers on two dice, whose product is a perfect square.
Solution:
Total number of cases = 36
Favourable cases are (1,1), (1,4), (2,2), (3, 3), (4,1), (4,4), (5,5), (6, 6)
![]()
Question 73.
A box contains 80 discs which are numbered from 1 to 80. If one disc is drawn at random from the box, find the probability that it bears a perfect square number.
Solution:
Total number of discs = 80
Numbers from 1 to 80 which are perfect square are 1, 4, 9,16, 25, 36, 49, 64.
Favourable number of dies =8
Required probability =8/80=1/10
Question 74.
Two dice are rolled once. Find the probability of getting such numbers on the two dice, whose product is 12.
Solution:
When two dice are rolled, total number of cases = 36
Number of favourable cases whose product is 12 are given as {(2,6), (3,4), (4,3), (6,2)}, i.e. 4
![]()
Question 75.
Cards marked with numbers 5,6,7, , 74 are placed in a bag and mixed thoroughly. One card is drawn at random from the bag. Find the probability that the number on the card is a perfect square.
Solution:
Total cards = 70
Perfect square numbers from 5 to 74 are 9,16, 25, 36, 49, 64.
Number of favourable cards = 6
P(a perfect square) =6/70=3/35
2010
Short Answer Type Questions I [2 Marks]
Question 76.
A card is drawn at random from a well-shuffled pack of 52 playing cards. Find the probability of getting a red face card.
Solution:
Total cases = 52
Favourable cases = 6 (red face cards, i.e. 2 kings, 2 queens, 2 jacks)
Probability of getting a red face card =6/52=3/26
Question 77.
A die is thrown once. What is the probability of getting a number greater than 4?
Solution:
Total cases = 6
Favourable cases for the numbers greater than 4 are 2 (i.e. 5, 6).
Probability of getting a number greater than 4=2/6=1/3
Question 78.
A die is thrown twice. What is the probability that the same number will come up either time?
Solution:
Total cases when die is thrown twice = 36
Favourable cases for same number either time = 6 i.e. (1,1), (2, 2), (3,3), (4,4), (5,5), (6, 6)
Probability of getting same number either time =6/36=1/6
Short Answer Type Questions II [3 Marks]
Question 79.
Cards bearing numbers 1,3,5,,,,35 are kept in a bag. A card is drawn at random from the bag. Find the probability of getting a card bearing
- a prime number less than 15.
- a number divisible by 3 and 5.
Solution:
Total number of cards in a bag = 18
- Prime numbers less than 15 are 3, 5, 7,11,13
Number of favourable cases = 5
P (a prime number less than 15) =5/18 - The number divisible by 3 and 5 in given number is 15.
Number of favourable cases = 1
P (a number divisible by 3 and 5)=1/18
Question 80.
A bag contains cards which are numbered from 2 to 90. A card is drawn at random from the bag. Find the probability that it bears
- a two-digit number,
- a number which is a perfect square.
Solution:
Total number of cards = 89
- Out of 89 cards, there are 8 single-digit numbers and 81 are two-digit numbers.
Number of favourable cases = 81
P (getting a two-digit number) = 81/89 - 4, 9,16, 25, 36,49, 64, 81 are 8 perfect square numbers from 2 to 90.
P (getting a perfect square number) =8/89
Question 81.
From a well-shuffled pack of playing cards, blackjacks, black kings and black aces are removed. A card is then drawn at random from the pack. Find the probability of getting
- a red card.
- not a diamond card
Solution:
As blackjacks, black kings and black aces are removed from the pack, so, number of remaining cards in a pack = 46
- Favourable cases of a red card are 26.
Probability of getting a red card = 26/46=13/23 - Favourable cases of not getting a diamond card are = 46 – 13 = 33
Probability of not getting a-diamond card =33/46