Contents
Selina Concise Mathematics Class 8 ICSE Solutions Chapter 16 Understanding Shapes (Including Polygons)
Selina Publishers Concise Mathematics Class 8 ICSE Solutions Chapter 16 Understanding Shapes (Including Polygons)
Understanding Shapes Exercise 16A – Selina Concise Mathematics Class 8 ICSE Solutions
Question 1.
State which of the following are polygons :

If the given figure is a polygon, name it as convex or concave.
Solution:

Question 2.
Calculate the sum of angles of a polygon with :
(i) 10 sides
(ii) 12 sides
(iii) 20 sides
(iv) 25 sides
Solution:

Question 3.
Find the number of sides in a polygon if the sum of its interior angles is :
(i) 900°
(ii) 1620°
(iii) 16 right-angles
(iv) 32 right-angles.
Solution:


Question 4.
Is it possible to have a polygon ; whose sum of interior angles is :
(i) 870°
(ii) 2340°
(iii) 7 right-angles
(iv) 4500°
Solution:


Question 5.
(i) If all the angles of a hexagon are equal ; find the measure of each angle.
(ii) If all the angles of a 14-sided figure are equal ; find the measure of each angle.
Solution:

Question 6.
Find the sum of exterior angles obtained on producing, in order, the sides of a polygon with :
(i) 7 sides
(ii) 10 sides
(iii) 250 sides.
Solution:


Question 7.
The sides of a hexagon are produced in order. If the measures of exterior angles so obtained are (6x – 1)°, (10x + 2)°, (8x + 2)° (9x – 3)°, (5x + 4)° and (12x + 6)° ; find each exterior angle.
Solution:
 >
>
Question 8.
The interior angles of a pentagon are in the ratio 4 : 5 : 6 : 7 : 5. Find each angle of the pentagon.
Solution:

Question 9.
Two angles of a hexagon are 120° and 160°. If the remaining four angles are equal, find each equal angle.
Solution:

Question 10.
The figure, given below, shows a pentagon ABCDE with sides AB and ED parallel to each other, and ∠B : ∠C : ∠D = 5 : 6 : 7.

(i) Using formula, find the sum of interior angles of the pentagon.
(ii) Write the value of ∠A + ∠E
(iii) Find angles B, C and D.
Solution:

Question 11.
Two angles of a polygon are right angles and the remaining are 120° each. Find the number of sides in it.
Solution:

Question 12.
In a hexagon ABCDEF, side AB is parallel to side FE and ∠B : ∠C : ∠D : ∠E = 6 : 4 : 2 : 3. Find ∠B and ∠D.
Solution:

Question 13.
the angles of a hexagon are x + 10°, 2x + 20°, 2x – 20°, 3x – 50°, x + 40° and x + 20°. Find x.
Solution:

Question 14.
In a pentagon, two angles are 40° and 60°, and the rest are in the ratio 1 : 3 : 7. Find the biggest angle of the pentagon.
Solution:

Understanding Shapes Exercise 16B – Selina Concise Mathematics Class 8 ICSE Solutions
Question 1.
Fill in the blanks :
In case of regular polygon, with :
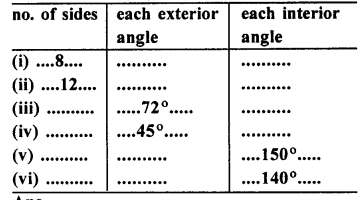
Solution:


Question 2.
Find the number of sides in a regular polygon, if its each interior angle is :
(i) 160°
(ii) 135°
(iii) \(1\frac { 1 }{ 5 }\) of a right-angle
Solution:


Question 3.
Find the number of sides in a regular polygon, if its each exterior angle is :
(i) \(\frac { 1 }{ 3 }\) of a right angle
(ii) two-fifth of a right-angle.
Solution:
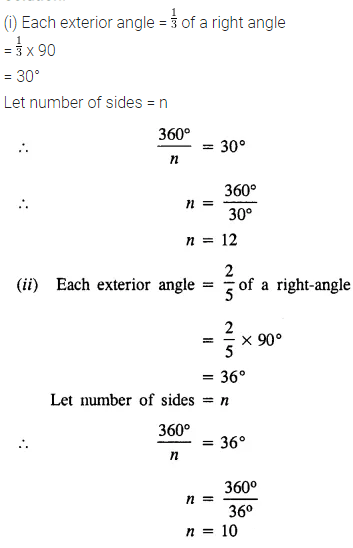
Question 4.
Is it possible to have a regular polygon whose each interior angle is :
(i) 170°
(ii) 138°
Solution:


Question 5.
Is it possible to have a regular polygon whose each exterior angle is :
(i) 80°
(ii) 40% of a right angle.
Solution:

Question 6.
Find the number of sides in a regular polygon, if its interior angle is equal to its exterior angle.
Solution:

Question 7.
The exterior angle of a regular polygon is one-third of its interior angle. Find the number of sides in the polygon.
Solution:


Question 8.
The measure of each interior angle of a regular polygon is five times the measure of its exterior angle. Find :
(i) measure of each interior angle ;
(ii) measure of each exterior angle and
(iii) number of sides in the polygon.
Solution:

Question 9.
The ratio between the interior angle and the exterior angle of a regular polygon is 2 : 1. Find :
(i) each exterior angle of the polygon ;
(ii) number of sides in the polygon
Solution:

Question 10.
The ratio between the exterior angle and the interior angle of a regular polygon is 1 : 4. Find the number of sides in the polygon.
Solution:

Question 11.
The sum of interior angles of a regular polygon is twice the sum of its exterior angles. Find the number of sides of the polygon.
Solution:

Question 12.
AB, BC and CD are three consecutive sides of a regular polygon. If angle BAC = 20° ; find :
(i) its each interior angle,
(ii) its each exterior angle
(iii) the number of sides in the polygon.
Solution:

Question 13.
Two alternate sides of a regular polygon, when produced, meet at the right angle. Calculate the number of sides in the polygon.
Solution:

Question 14.
In a regular pentagon ABCDE, draw a diagonal BE and then find the measure of:
(i) ∠BAE
(ii) ∠ABE
(iii) ∠BED
Solution:

Question 15.
The difference between the exterior angles of two regular polygons, having the sides equal to (n – 1) and (n + 1) is 9°. Find the value of n.
Solution:
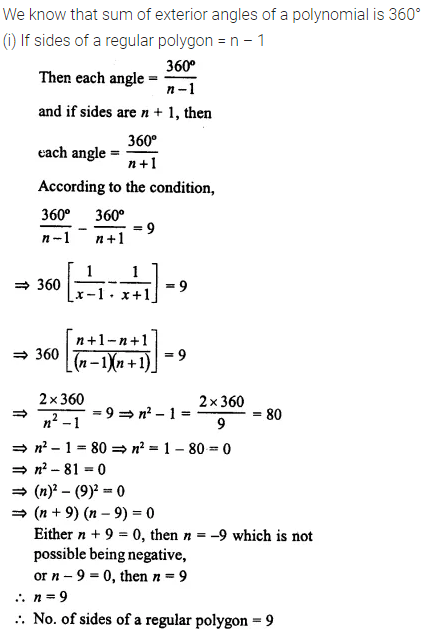
Question 16.
If the difference between the exterior angle of a n sided regular polygon and an (n + 1) sided regular polygon is 12°, find the value of n.
Solution:

Question 17.
The ratio between the number of sides of two regular polygons is 3 : 4 and the ratio between the sum of their interior angles is 2 : 3. Find the number of sides in each polygon.
Solution:
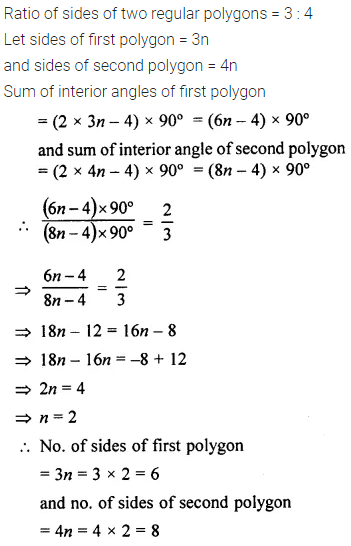
Question 18.
Three of the exterior angles of a hexagon are 40°, 51 ° and 86°. If each of the remaining exterior angles is x°, find the value of x.
Solution:

Question 19.
Calculate the number of sides of a regular polygon, if:
(i) its interior angle is five times its exterior angle.
(ii) the ratio between its exterior angle and interior angle is 2 : 7.
(iii) its exterior angle exceeds its interior angle by 60°.
Solution:

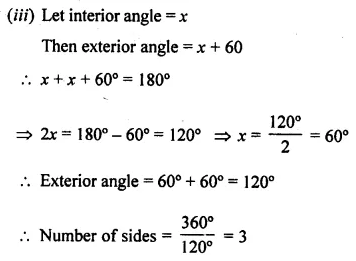
Question 20.
The sum of interior angles of a regular polygon is thrice the sum of its exterior angles. Find the number of sides in the polygon.
Solution:

Understanding Shapes Exercise 16C – Selina Concise Mathematics Class 8 ICSE Solutions
Question 1.
Two angles of a quadrilateral are 89° and 113°. If the other two angles are equal; find the equal angles.
Solution:

Question 2.
Two angles of a quadrilateral are 68° and 76°. If the other two angles are in the ratio 5 : 7; find the measure of each of them.
Solution:

Question 3.
Angles of a quadrilateral are (4x)°, 5(x + 2)°, (7x – 20)° and 6(x + 3)°. Find :
(i) the value of x.
(ii) each angle of the quadrilateral.
Solution:

Question 4.
Use the information given in the following figure to find :
(i) x
(ii) ∠B and ∠C

Solution:
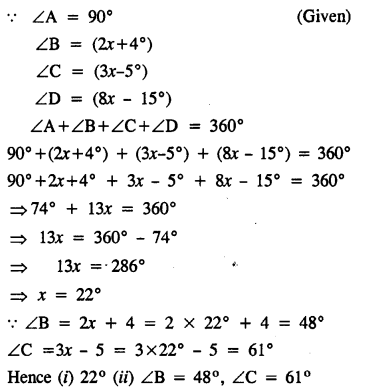
Question 5.
In quadrilateral ABCD, side AB is parallel to side DC. If ∠A : ∠D = 1 : 2 and ∠C : ∠B = 4 : 5
(i) Calculate each angle of the quadrilateral.
(ii) Assign a special name to quadrilateral ABCD
Solution:
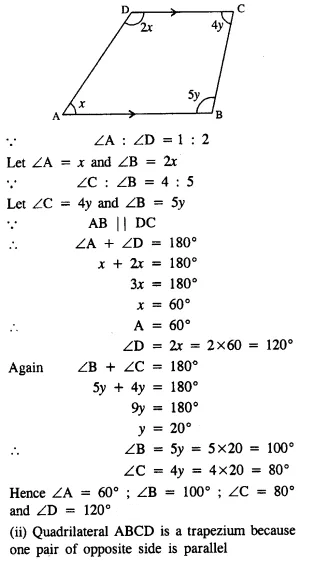
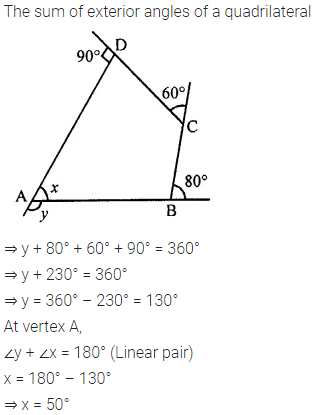
Question 6.
From the following figure find ;
(i) x
(ii) ∠ABC
(iii) ∠ACD
Solution:

Question 7.
Given : In quadrilateral ABCD ; ∠C = 64°, ∠D = ∠C – 8° ; ∠A = 5(a + 2)° and ∠B = 2(2a + 7)°.
Calculate ∠A.
Solution:

Question 8.
In the given figure : ∠b = 2a + 15 and ∠c = 3a + 5; find the values of b and c.

Solution:

Question 9.
Three angles of a quadrilateral are equal. If the fourth angle is 69°; find the measure of equal angles.
Solution:

Question 10.
In quadrilateral PQRS, ∠P : ∠Q : ∠R : ∠S = 3 : 4 : 6 : 7.
Calculate each angle of the quadrilateral and then prove that PQ and SR are parallel to each other
(i) Is PS also parallel to QR?
(ii) Assign a special name to quadrilateral PQRS.
Solution:

Question 11.
Use the informations given in the following figure to find the value of x.

Solution:

Question 12.
The following figure shows a quadrilateral in which sides AB and DC are parallel. If ∠A : ∠D = 4 : 5, ∠B = (3x – 15)° and ∠C = (4x + 20)°, find each angle of the quadrilateral ABCD.

Solution:

Question 13.
Use the following figure to find the value of x

Solution:
Question 14.
ABCDE is a regular pentagon. The bisector of angle A of the pentagon meets the side CD in point M. Show that ∠AMC = 90°.
Solution:

Question 15.
In a quadrilateral ABCD, AO and BO are bisectors of angle A and angle B respectively. Show that:
∠AOB = \(\frac { 1 }{ 2 }\) (∠C + ∠D)
Solution:
