Triangles Class 10 Maths CBSE Important Questions With Solutions

Important Questions for Class 10 Maths Chapter 6 Triangles with solutions includes all the important topics with detailed explanation that aims to help students to score more marks in Board Exams 2020. Students who are preparing for their Class 10 exams must go through Important Questions for Class 10 Math Chapter 6 Triangles.

Important Questions for Class 10 Maths Chapter 6 Triangles

Expert teachers at CBSETuts.com collected and solved 2 Marks and 4 mark important questions for Class 10 Maths Chapter 6 Triangles.

MathsScienceEnglishSocialHindi AHindi B

2016

Very Short Answer Type Question [1 Mark]

Question 1.
If A ABC ~ ARPQ, AB = 3 cm, BC = 5 cm, AC = 6 cm, RP = 6 cm and PQ = 10 cm, then find QR
Solution:

Short Answer Type Question I [2 Marks]

Question 2.
R and S are points on the sides DE and EF respectively of a ADEF such that ER = 5 cm, RD = 2.5 cm, SE = 1.5 cm and FS = 3.5 cm. Find whether RS || DF or not.
Solution:

Short Answer Type Questions II [3 Marks]

Question 3.
From airport two aeroplanes start at the same time. If the speed of first aeroplane due North is 500 km/h and that of other due East is 650 km/h, then find the distance between two aeroplanes after 2 hours.
Solution:

Question 4.
AABC, is right angled at C. If p is the length of the perpendicular from C to AB and a, b, c are the lengths of the sides opposite ∠A,∠B, ∠C respectively then prove that
Solution:

Question 5.
In the figure, ABCD is a parallelogram and E divides BC in the ratio 1: 3. DB and AE intersect at F. Show that DF = 4FB and AF = 4FE
Solution:

Long Answer Type Questions [4 Marks]

Question 6.
State and prove Converse of Pythagoras’ Theorem.
Solution:

Question 7.
In the figure, PQR and QST respectively. Prove that QR X QS= QP X QT
Solution:

2015

Very Short Answer Type Question [1 Mark]

Question 8.
In ADEW, AB || EW. If AD = 4 cm, DE = 12 cm and DW = 24 cm, then find the value of DB.
Solution:

Short Answer Type Question I [2 Marks]

Question 9.
A ladder is placed against a wall such that its foot is at distance of 5 m from the wall and its top reaches a window 5/3 m above the ground. Find the length of the ladder
Solution:

Short Answer Type Questions II [3 Marks]

Question 10.
In figure, if ∠CAB = ∠CED, then prove that AB X DC = ED X BC.
Solution:

Question 11.
State whether the given pairs of triangles are similar or not. In mention the criterion.
Solution:

Long Answer Type Questions [4 Marks]

Question 12.
In ∆ABC, from A and B altitudes AD and BE are drawn. Prove that ∆ADC ~ ∆BEC. Is ∆ADB ~ ∆AEB and ∆ADB ~ ∆ADC?
Solution:

Question 13.
In ∆ABC, if ∠ADE = ∠B, then prove that ∆ADE ~ ∆ABC. Also, if AD = 7.6 cm, AE = 7.2 cm, BE = 4.2 cm and BC = 8.4 cm, then find DE.
Solution:

2014

Very Short Answer Type Questions [1 Mark]

Question 14.
If ∆ABC ~ ∆RPQ, AB = 3 cm, BC = 5 cm, AC = 6 cm, RP = 6 cm and PQ = 10 cm, then find QR.
Solution:

Question 15.
Let  ∆ABC ~ ∆DEF, ar (∆ABC) = 169 cm2 and ar (∆DEF) = 121 cm². If AB = 26 cm² then find DE.
Solution:

Question 16.
If in an equilateral triangle, the length of the median is √3 cm, then find the length of the side of equilateral triangle.
Solution:

Short Answer Type Questions I [2 Marks]

Question 17.
In the figure, D andE are points on AB and AC respectively such that DE||BC. If AD = 1/3 BD and AE = 4.5 cm, find AC.
Solution:

Question 18.
Determine whether the triangle having sides (a – 1) cm, 2 √a cm and (a + 1) cm is a right angled triangle.
Solution:

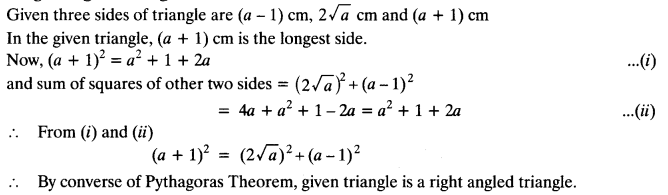
Question 19.
In an equilateral triangle of side 3√3 cm, find the length of the altitude.
Solution:

Short Answer Type Questions II [3 Marks]

Question 20.
In the figure, ABC is a triangle and BD ⊥ AC. Prove that AB² + CD² = AD² + BC²
Solution:

Question 21.
Right angled triangles BAC and BDC are right angled at A and D and they are on same side of BC. If AC and BD intersect at P, then prove that AP x PC = PB X DP.
Solution:

Question 22.
In the given figure, if LM || CB and LN|| CD, prove that AM X AD = AB X AN.
Solution:

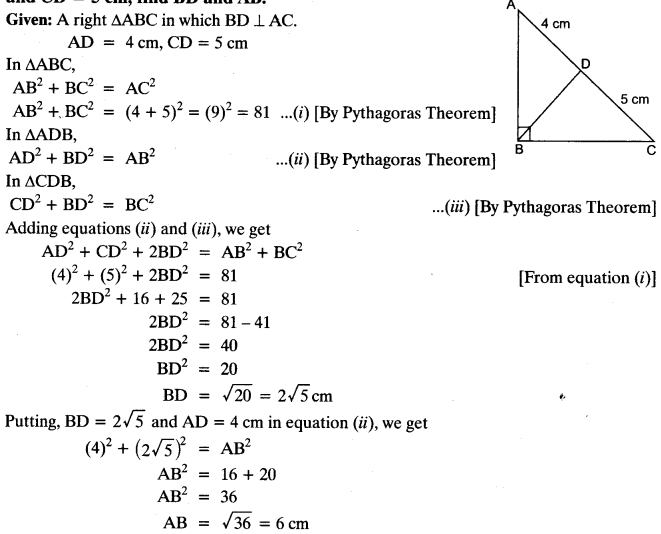
Question 23.
In the given figure, ABC is a triangle, right angled at B and BD⊥AC. If AD = 4 cm and CD = 5 cm, find BD and AB.
Solution:

Question 24.
Equiangular triangles are drawn on sides of right angled triangle in which perpendicular is double of its base. Show that area of triangle on the hypotenuse is the sum of areas of the other two triangles?
Solution:

Question 25.
If in a right angle AABC, right angled at A, AD ⊥ BC, then prove that AB² + CD² = BD² + AC²
Solution:

Long Answer Type Questions [4 Marks]

Question 26.
Prove that the ratio of the areas of two similar triangles is equal to the ratio of squares of their corresponding sides.
Solution:

Question 27.
In ∆ABC, AX⊥ BC and Y is middle point of BC. Then prove that,

Solution:

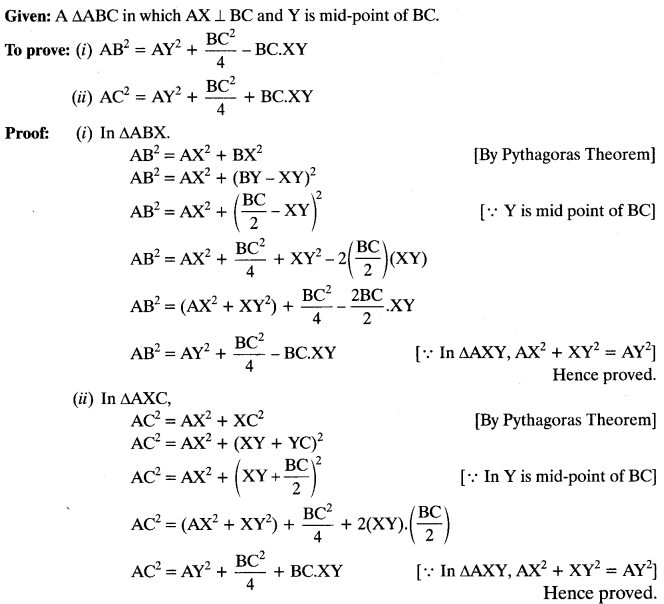
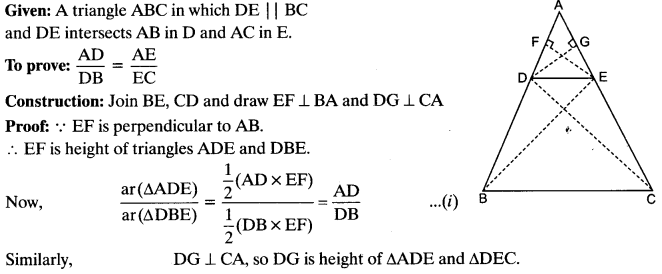
Question 28.
Prove that if a line is drawn parallel to one side of a triangle to intersect the othertwo sides at distinct points, then other two sides are divided in the same ratio.
Solution:

Question 29.
Prove that the sum of square of the sides of a rhombus is equal to the sum of squares of its diagonals.
Solution:

Question 30.
In AABC, X is any point on AC. If Y, Z , U and Y are the middle points of AX, XC, AB and BC respectively, then prove that UY || VZ and UV|| YZ.
Solution:

Question 31.
In ∆ABC, ZB = 90°, BD ⊥ AC, ar (∆ABC) = A and BC = a, then prove that

Solution:

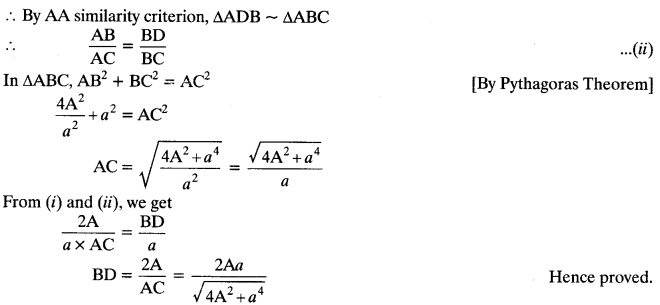
2013

Short Answer Type Questions I [2 Marks]

Question 32.
In the figure, PQR and SQR are two right triangles with common hypotenuse QR. If PR and SQ intersect at M such that PM = 3 cm, MR = 6 cm and SM = 4 cm, find the length of MQ.
Solution:

Question 33.
Find the length of each altitude of an equilateral triangle
Solution:

Short Answer Type Questions Il [3 Marks]

Question 34.
In the figure, DB⊥BC, DE⊥AB and AC⊥ BC prove that

Solution:

Question 35.
In the given figure, ABCD is a rectangle. P is the mid-point of DC. If QB = 7 m, AD = 9 cm and DC = 24 cm, then prove that ∠APQ = 90°
Solution:

Question 36.
In AABC, D, E and F are the mid-points of AB, BC and AC respectively. Find the ratio of area of ∆ABC and area of ∆DEF.
Solution:

Long Answer Type Questions [4 Marks]

Question 37.
In the figure, ABC is a right triangle, right angled at B. AD and CF are two medians drawn from A and C respectively. If AC = 5 cm and AD = 3√5/2cm. Find the length of CE.
Solution:

Question 38.
ABC is a right triangle, right-angled at B. D and E trisect BC, prove that 8AE² = 3AC² + 5 AD²
Solution:

Question 39.
Prove that in a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then the angle opposite the first side is a right angle.
Solution:

Question 40.
In ∆ABC, AD is the median to BC and in ∆PQR, PM is the median to QR.

Solution:

2012

Short Answer Type Question I [2 Marks]

Question 41.
In the given figure, if AB || DC, find the value of x.
Solution:

Short Answer Type Question II [3 Marks]

Question 42.
In the given figure PQ || BA; PR || CA. If PD = 12 cm. Find BD X CD.
Solution:

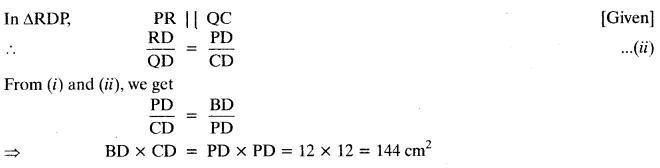
2011

Short Answer Type Question I [2 Marks]

Question 43.
If one diagonal of a trapezium divides the other diagonal in the ratio 1 : 3. Prove that one of the parallel sides is three times the other.
Solution:

Short Answer Type Questions II [3 Marks]

Question 44.
In given figure ∆ABC is similar to ∆XYZ and AD and XE are angle bisectors of ∠A and ∠X respectively such that AD and XE in centimetres are 4 and 3 respectively, find the ratio of area of ∆ABD and area of ∆XYE.
Solution:

Question 45
In figure, AB || PQ || CD, AB = x units, CD =y units and PQ = z units, prove that

Solution:

Long Answer Type Questions [4 Marks]

Question 46.
The area of two similar triangles are 49 cm² and 64 cm² respectively. If the difference of the corresponding altitudes is 10 cm, then find the lengths of altitudes (in centimetres).
Solution:

Question 47.
In an equilateral triangle ABC, D is a point on side BC such that 4BD = BC. Prove that ADcm² = BCcm².
Solution:

2010

Very Short Answer Type Questions [1 Mark]

Question 48.
In figure, S and T are points on the sides PQ and PR, respectively of APQR, such that PT = 2 cm, TR = 4 cm and ST is parallel to QR. Find the ratio of the areas of ∆PST and ∆PQR.
Solution:

Question 49.
In figure, DE || BC in AABC such that that BC = 8 cm, AB = 6 cm and DA = 1.5 cm. Find DE.
Solution:

Question 50.
In figure, MN || AB, BC = 7.5 cm, AM = 4 cm and MC = 2 cm. Find the length BN.
Solution:

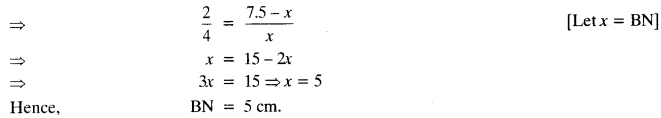
Short Answer Type Questions I [2 Marks]

Question 51.
Triangle ABC is right angled at B, and D is mid-point of BC. Prove that AC² = 4AD² – 3AB².
Solution:

Question 52.
If BL and CM are medians of a triangle ABC right angled at A, then prove that4(BL² + CM²) = 5BC².
Solution:

Question 53.
In figure, a triangle ABC is drawn to circumscribe a circle of radius 3 cm, such that the segments BD and DC into which BC is divided by the point of contact D are of lengths 6 cm and 8 cm respectively. Find the side AB if the area of ∆ABC = 63 cm2.
Solution:

Short Answer Type Question II [3 Marks]

Question 54.
In figure, ABC is an isosceles triangle in which AB = AC. E is a point on the side CB produced, such that FE ⊥ AC. If AD ⊥ CB, prove that AB X EF = AD X EC.
Solution:

Long Answer Type Questions [4 Marks]

Question 55.
Prove that in a right angle triangle the square on the hypotenuse is equal to the sum of the squares on the other two sides. Point D is the mid-point of the side BC of a right triangle ABC, right angled at C. Prove that, 4AD² = 4AC² + BC²..
Solution:

Question 56.
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.
Using the above, prove the following:
If the areas of two similar triangles are equal, then prove that the triangles are congruent.
Solution:

Question 57.
In a triangle, if the square of one side is equal to the sum of the squares of the other two sides, then prove that the angle opposite the first side is a right angle.
Using the above, do the following:
In an isosceles triangle PQR, PQ = QR and PR² = 2PQ². . Prove that ZQ is a right angle.
Solution:

Question 58.
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
Using the above, do the following:
In figure, BA || QR, and CA || SR, prove
Solution:

Question 59.
Prove that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. Using the above, do the following:
AD is an altitude of an equilateral triangle ABC. On AD as base, another equilateral triangle ADE is constructed. Prove that, area (∆ADE): area (∆ABC) =3:4
Solution:

Question 60.
If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, prove that the other two sides are divided in the same ratio.
Using the above, do the following:
In figure, PQ || AB and AQ || CB.
Prove that AR² = PR. CR.
Solution:

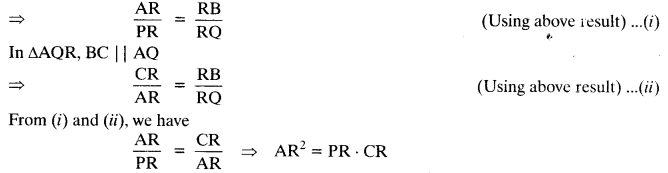
2009

Very Short Answer Type Questions [1 Mark]

Question 61.
In fig. ∠M =∠N = 46°, express JC in terms of a, b andc, where a, andc are lengths ofLM, MN and NK respectively.
Solution:

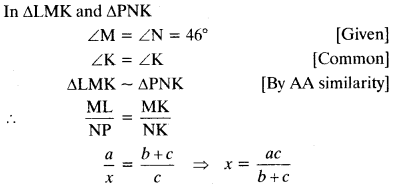
Question 62.
If the areas of two similar triangles are in ratio 25 : 64, write the ratio of their corresponding sides.
Solution:

Question 63.
In a ∆ABC, DE || BC. If DE = – BC and area of ∆ABC = 81 cm2, find the area of ∆ADE.
Solution:

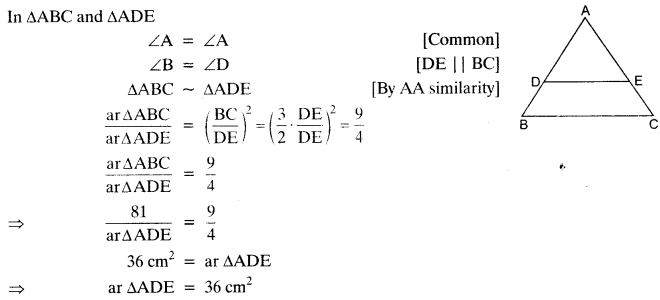
Short Answer Type Questions I [2 Marks]

Question 64.
In figure,∆ABD is a right triangle, right angled at A and AC⊥BD. Prove that AB² = BC.BD.
Solution:

Question 65.
In figure, S and T trisect the side QR of a right triangle PQR.Prove that 8PT² = 3PR² + 5PS².
Solution:

Short Answer Type Questions II [3 Marks]

Question 66.
In figure, AABC is right angled at C and DE ⊥ AB. Prove that ∆ABC ~ ∆ADE and hence find the lengths of AE and DE.
Solution:

Question 67.
In figure, DEFG is a square and ∠BAC = 90°. Show that DE² = BD X EC.
Solution:

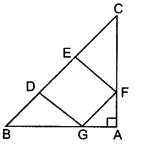
Question 68.
In figure, AD ⊥ BC and BD = 1/3 CD.
Prove that 2CA² = 2AB² + BC².
Solution:

Question 69.
In figure, M is mid-point of side CD of a parallelogram ABCD. The line BM is drawn intersecting AC at L and AD produced at E. Prove that EL = 2BL.
Solution:

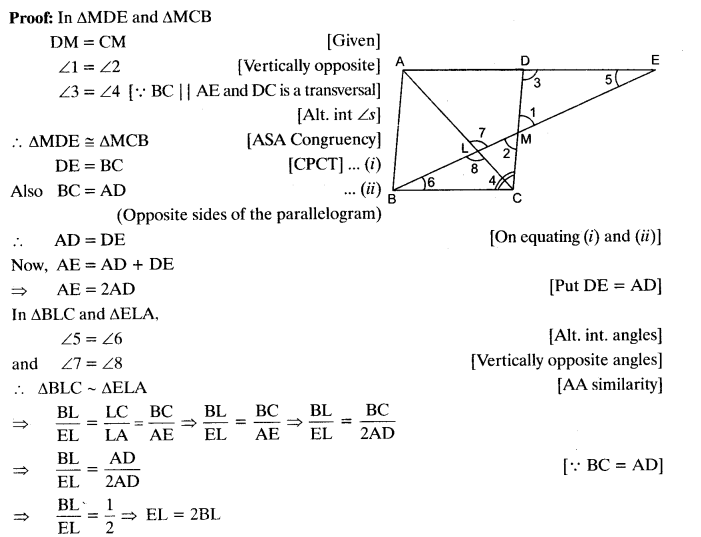
Question 70.
In figure, two triangles ABC and DBC lie on the same side of base BC. P is a point on BC such that PQ || BA and PR || BD. Prove that QR || AD.
Solution:

Long Answer Type Questions [4 Marks]

Question 71.
Prove that the ratio of areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
Using the above, do the following:
In a trapezium ABCD, AC and BD intersecting at O, AB|| DC and AB = 2CD, if area of ∆AOB = 84 cm2, find the area of ∆COD
Solution:

Question 72.
Prove that in a right angle triangle the square on the hypotenuse is equal to the sum of the squares on the other two sides. ‘
Using the above, do the following:
Prove that in a ∆ABC, if AD is perpendicular to BC, then AB² + CD² = AC² + BD².
Solution:

Question 73.
Prove that if a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points, the other two sides are divided is the same ratio.
Using the above result, do the following:
In figure, DE|| BC and BD = CE. Prove that ∆ABC is an isosceles triangle.
Solution:

Question 74.
Prove that the ratio of areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.
Using the above, prove the following: The areas of the equilateral triangle described on the side of a square is half the area of the equilateral triangle described, on its diagonal.
Solution:

Question 75.
AABC is an isosceles triangle in which AC = BC. If AB²  =   2AC² then, prove that ∆ABC is right triangle.
Solution: