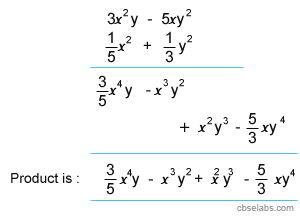Contents
In the multiplication of two binomials, we will use the distributive property of multiplication of literals over their addition.
Let us consider, two binomials say (a + b) and (c + d). By using the distributive property of multiplication of literals over their addition, we have
(a + b) x (c + d) = a x (c + d) + b x (c + d)
= (a x c + a x d) + (b x c + b x d)
= ac + ad + bc + bd.
To multiply any two binomials, we multiply each term of one binomial with every term of the other binomial and add all the products so obtained.
Multiplication of two binomials by horizontal method:
Step 1) Write the each binomial expression inside the parentheses separated by a multiplication symbol.
Step 2) Now multiply each term of one binomial with every term of the other binomial expression.
Step 3) The result is the sum of the products obtained in Step (2).
Multiplication of two binomials by vertical method:
Step 1) Write the expressions one below the other such that the expression to be multiplied comes in the second row and the like terms come one below the other.
Step 2) Multiply each term of one binomial with each term of another binomial.
Step 3) Write the result below the concerned column.
Step 4) The result is the sum of the products obtained below each column.
Multiplication of Two Binomials Example1:
Multiply (3a + 2b) by (5a + 7b).
Solution: By Horizontal method: We have, (3a + 2b) x (5a + 7b)
= 3a(5a + 7b) + 2b(5a + 7b)
= (3a x 5a) + (3a x 7b) + (2b x 5a) + (2b x 7b)
= 15\(a^2\) + 21ab + 10ba + 14\(b^2\)
= 15\(a^2\) + 31ab + 14\(b^2\).
By vertical method:
First, multiply 3a + 2b by 5a
Next, multiply 3a + 2b by 7b
Finally, add the like terms.
Multiplication of Two Binomials Example2:
Multiply \(2x^2 + 3y^2\) by \(5x^2 – y^2\).
Solution: By horizontal method: We have, \(2x^2 + 3y^2\) x \(5x^2 – y^2\)
= \(2x^2\)(\(5x^2 – y^2\)) + \(3y^2\)(\(5x^2 – y^2\))
= \(10x^4 – 2x^2y^2 + 15x^2y^2 – 3y^4\)
= \(10x^4 + 13x^2y^2 – 3y^4\).
By vertical method:
First, multiply \(2x^2 + 3y^2\) by \(5x^2\)
Next, multiply \(2x^2 + 3y^2\) by \(-y^2\)
Finally, add the like terms.
Multiplication of Two Binomials Example3:
Multiply \(3x^2 – 5y^2\) by \(\frac{1}{5}{x^2} + \frac{1}{3}{y^2}\)
Solution: By horizontal method: We have, \(\frac{1}{5}{x^2} + \frac{1}{3}{y^2}\) x \(3x^2 – 5y^2\)
= \(\frac{1}{5}{x^2}(3x^2 – 5y^2) + \frac{1}{3}{y^2}(3x^2 – 5y^2)\)
= \(\frac{3}{5}{x^4}y – {x^3}{y^2} + {x^2}{y^3} – \frac{5}{3}x{y^4}\)
By vertical method:
First, multiply \(3x^2 – 5y^2\) by \(\frac{1}{5}{x^2}\)
Next, multiply \(3x^2 – 5y^2\) by \(\frac{1}{3}{y^2}\)
Finally, add the like terms.
Remark: Whenever, you have to find the product of two binomials, you can shorten and quicken your work by multiplying the two binomials mentally i.e., by horizontal (or) row method.
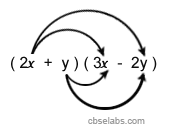
Multiplication of Two Binomials Example4:
Multiply (2x + y) by (3x – y).
Solution:
First multiply by 2x = \(6x^2 – 4xy\)
Then multiply by y = \(3xy – 2y^2\)
= \(6x^2 – 4xy + 3xy – 2y^2\)
By combining -4xy and 3xy mentally we obtain -xy.
The product is \(6x^2 – xy – 2y^2\).
Multiplication of Two Binomials Example5:
Multiply \(3a^2 – 4b^2c\) by \(5a^2 – 7b^2c\).
Solution:
First multiply by \(3a^2\) = \(15a^4 – 21a^2b^2c\)
Then multiply by \(-4b^2c\) = \(– 20a^2b^2c + 28b^4c^2\)
= \(15a^4 – 21a^2b^2c – 20a^2b^2c + 28b^4c^2\)
By combining \(– 21a^2b^2c\) and \(– 20a^2b^2c\) mentally we obtain \(– 41a^2b^2c\).
The product is \(15a^4 – 41a^2b^2c + 28b^4c^2\).