CBSE Tuts

CBSE Maths notes, CBSE physics notes, CBSE chemistry notes

NCERT Solutions for Class 12 Maths Chapter 9 Differential Equations Ex 9.3

NCERT Solutions for Class 12 Maths Chapter 9 Differential Equations Ex 9.3 are part of NCERT Solutions for Class 12 Maths. Here we have given NCERT Solutions for Class 12 Maths Chapter 9 Differential Equations Ex 9.3.

Board CBSE
Textbook NCERT
Class Class 12
Subject Maths
Chapter Chapter 9
Chapter Name Differential Equations
Exercise Ex 9.3
Number of Questions Solved 12
Category NCERT Solutions

NCERT Solutions for Class 12 Maths Chapter 9 Differential Equations Ex 9.3

In each of the following, Q. 1 to 5 form a differential equation representing the given family of curves by eliminating arbitrary constants a and b.

Ex 9.3 Class 12 Maths Question 1.
\frac { x }{ a } +\frac { y }{ b } =1
Solution:
Given that \frac { x }{ a } +\frac { y }{ b } =1 …(i)
differentiating (i) w.r.t x, we get
\frac { 1 }{ a } +\frac { 1 }{ b } { y }^{ I }=0 …(ii)
again differentiating w.r.t x, we get
\frac { 1 }{ b } { y }^{ II }=0\Rightarrow { y }^{ II }=0
which is the required differential equation

Ex 9.3 Class 12 Maths Question 2.
y² = a(b² – x²)
Solution:
given that
y² = a(b² – x²)…(i)
NCERT Solutions for Class 12 Maths Chapter 9 Differential Equations 2
NCERT Solutions for Class 12 Maths Chapter 9 Differential Equations 2.1

Ex 9.3 Class 12 Maths Question 3.
y = ae3x+be-2x
Solution:
Given that
y = ae3x+be-2x …(i)
NCERT Solutions for Class 12 Maths Chapter 9 Differential Equations 3

Ex 9.3 Class 12 Maths Question 4.
y = e2x (a+bx)
Solution:
y = e2x (a+bx)
NCERT Solutions for Class 12 Maths Chapter 9 Differential Equations 4

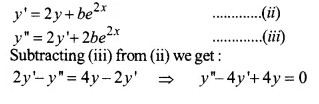
Ex 9.3 Class 12 Maths Question 5.
y = ex(a cosx+b sinx)
Solution:
The curve y = ex(a cosx+b sinx) …(i)
differentiating w.r.t x
byjus class 12 maths Chapter 9 Differential Equations 5

Ex 9.3 Class 12 Maths Question 6.
Form the differential equation of the family of circles touching the y axis at origin
Solution:
The equation of the circle with centre (a, 0) and radius a, which touches y- axis at origin
NCERT Solutions for Class 12 Maths Chapter 9 Differential Equations 6

Ex 9.3 Class 12 Maths Question 7.
Form the differential equation of the family of parabolas having vertex at origin and axis along positive y-axis.
Solution:
The equation of parabola having vertex at the origin and axis along positive y-axis is
NCERT Solutions for Class 12 Maths Chapter 9 Differential Equations 7

Ex 9.3 Class 12 Maths Question 8.
Form the differential equation of family of ellipses having foci on y-axis and centre at origin.
Solution:
The equation of family ellipses having foci at y- axis is
NCERT Solutions for Class 12 Maths Chapter 9 Differential Equations 8

Ex 9.3 Class 12 Maths Question 9.
Form the differential equation of the family of hyperbolas having foci on x-axis and centre at the origin.
Solution:
Equation of the hyperbola is \frac { { x }^{ 2 } }{ { a }^{ 2 } } -\frac { { y }^{ 2 } }{ { b }^{ 2 } } =1
Differentiating both sides w.r.t x
byjus class 12 maths Chapter 9 Differential Equations 9
which is the req. differential eq. of the hyperbola.

Ex 9.3 Class 12 Maths Question 10.
Form the differential equation of the family of circles having centre on y-axis and radius 3 units
Solution:
Let centre be (0, a) and r = 3
Equation of circle is
x² + (y – a)² = 9 …(i)
Differentiating both sides, we get
NCERT Solutions for Class 12 Maths Chapter 9 Differential Equations 10
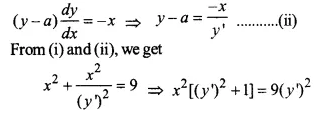
which is required equation

Ex 9.3 Class 12 Maths Question 11.
Which of the following differential equation has y={ c }_{ 1 }{ e }^{ x }+{ c }_{ 2 }{ e }^{ -x } as the general solution ?
(a) \frac { { d }^{ 2 }y }{ { dx }^{ 2 } } +y=0
(b) \frac { { d }^{ 2 }y }{ { dx }^{ 2 } } -y=0
(c) \frac { { d }^{ 2 }y }{ { dx }^{ 2 } } +1=0
(d) \frac { { d }^{ 2 }y }{ { dx }^{ 2 } } -1=0
Solution:
(b) y={ c }_{ 1 }{ e }^{ x }+{ c }_{ 2 }{ e }^{ -x }\Rightarrow \frac { dy }{ dx } ={ c }_{ 1 }{ e }^{ x }-{ c }_{ 2 }{ e }^{ -x }
\frac { { d }^{ 2 }y }{ { dx }^{ 2 } } ={ c }_{ 1 }{ e }^{ x }+{ c }_{ 2 }{ e }^{ -x }\Rightarrow \frac { { d }^{ 2 }y }{ { dx }^{ 2 } } -y=0

Ex 9.3 Class 12 Maths Question 12.
Which of the following differential equations has y = x as one of its particular solution ?
(a) \frac { { d }^{ 2 }y }{ { dx }^{ 2 } } -{ x }^{ 2 }\frac { dy }{ dx } +xy=x
(b) \frac { { d }^{ 2 }y }{ { dx }^{ 2 } } +{ x }\frac { dy }{ dx } +xy=x
(c) \frac { { d }^{ 2 }y }{ { dx }^{ 2 } } -{ x }^{ 2 }\frac { dy }{ dx } +xy=0
(d) \frac { { d }^{ 2 }y }{ { dx }^{ 2 } } +{ x }\frac { dy }{ dx } +xy=0
Solution:
(c) y = x
\frac { dy }{ dx } =1,\frac { { d }^{ 2 }y }{ { dx }^{ 2 } } =0
\frac { { d }^{ 2 }y }{ { dx }^{ 2 } } -{ x }^{ 2 }\frac { dy }{ dx } +xy=0

We hope the NCERT Solutions for Class 12 Maths Chapter 9 Differential Equations Ex 9.3 help you. If you have any query regarding NCERT Solutions for Class 12 Maths Chapter 9 Differential Equations Ex 9.3, drop a comment below and we will get back to you at the earliest.