Contents
The study of Physics Topics can help us understand and solve real-world problems, from climate change to medical imaging technology.
What is the Surface Energy and Surface Tension?
Surface Tension of Liquids
All liquids possess a special property—a tendency to minimise its surface area. This tendency of a liquid surface to contract its area is called surface tension. From our practical experience, we know that water droplets, or a small amount of mercury always takes the shape of a sphere. In the absence of external forces, all liquids always take a spherical, shape. For a given volume, the surface area of a sphere is the least and hence a liquid drop has a natural tendency to take the shape of a sphere.
If a clean dry needle is placed horizontally on the surface of water, then it is observed that the needle floats on water. The water surface under the needle is slightly depressed.
Insects like spiders and mosquitoes are able to walk on the surface of water. Where their legs touch, the water surface becomes slightly depressed.
From such observations, it seems that the surface of water behaves like a streched rubber membrane.
Experimental demonstration: A wire loop is dipped into a soap solution. A thin soap film will be formed in the loop when it is taken out of the solution. This film acts as the free surface of the liquid. A wet cotton thread loop, after being dipped in soap solution, is put on the film. No change is seen in the shape of the loop [Fig.(a)]. The soap film inside the loop is now punctured with a fine needle and it is observed that the cotton thread pulls itself into a circle [Fig. (b)]. What is the reason behind this observation?

Initially, there was soap film inside and outside the cotton loop. Every point on the Loop experienced equal and opposite forces tangential to the surface of the film. These two forces balanced each other. As a result, no resultant force acted on the loop.
After the film inside the loop was removed, the inward force vanished and only the film outside the loop exerted a force on the thread. We know that among all plane surfaces having the same boundary length, the area of a circle is the greatest.
Hence, a circle formed by the loop occupies the maximum area. So, the area of the film in between the loop and the thread reduces to a minimum. From this, it can be inferred clearly that the film has a tendency to minimise its area.
It can be concluded that a tension always acts on the free surface of a liquid and that the free surface behaves as a stretched thin membrane. Due to this tension, the free surface of any liquid has a tendency to contract so as to occupy the minimum area. This tension is known as surface tension.
Surface tension: Surface tension is the property of the free surface of a liquid due to which the liquid behaves as a stretched thin membrane and has a tendency to contract so as to minimise the surface area.
As a reason behind the origin of surface tension, it can be said that the molecules of a liquid attract each other by cohesive force [the force of attraction which acts between the molecules of same material is called cohesive force].
Equal cohesive force acts on the molecule inside the liquid from all directions.
Consequently, the resultant cohesive force on the molecule is zero. But, no cohesive forces act on the molecules of the free surface of the liquid to the outward direction. So, the cohesive force inside the liquid is not balanced. As a result, a resultant cohesive force acts on each molecule of the free surface in the downward direction. Thus, the free surface of a liquid tends to have the least surface area.
Let us imagine a straight line on the free surface of a liquid [Fig.]. Due to the tendency of the liquid surface to contract, the molecules on the opposite sides of the line try to move away from each other. This can be seen in the following experiment.

If a matchstick is placed on a water surface, it remains at rest. But when a drop of alcohol is put on water on one side of the stick, the stick moves in the opposite direction.
- The water surface exerts an equal pressure on both sides of the stick. This force is normal to the stick.
- When a drop of alcohol is put on water, the force on that side is weaker and the stick is pulled away by the stronger tangential force towards the opposite side.
Hence, surface tension can also be defined as follows:
Definition: The tangential force per unit length on a liquid surface, that acts along the normal on either side of an imaginary line on that surface, is called the surface tension of the liquid.
Units:

Dimension:

Surface Energy
We know that on the free surface of a liquid, the surface tension always tries to minimize the surface area. So, to increase the area of the surface of the liquid, an external force is needed. The external force does work to increase the area of the surface of the liquid, and the work done remains stored inside the surface of the liquid as potential energy.
The surface energy of a liquid is measured by the work done to increase the area of the surface of a liquid by unity.
Units:

Dimension:
[Surface energy] = \(\frac{[\text { work] }}{\text { [area] }}\) = \(\frac{\mathrm{ML}^2 \mathrm{~T}^{-2}}{\mathrm{~L}^2}\) = MT-2
Relation between surface tension and surface energy: A rectangular wire frame PQRS is taken. A wire AB can move along PQ and SR [Fig.]. When the frame is dipped into a soap solution and taken out a thin film is formed within the frame. As a result, the surface tension acts normally on the wire AB and tangentially to the surface of the film. This force tries to contract the film surface and pulls the wire AB towards QR. To keep the wire AB in its position, an equal but opposite force needs to be applied on it.
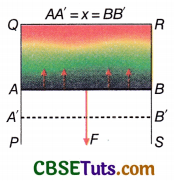
Let the length of the wire AB be l; surface tension of the liquid be T.
∴ The net force acting on the wire AB in the direction QR = 2lT. [The film has two surfaces and surface tension acts on each surface, therefore the net force has the factor of 2]
∴ To keep the wire AB still, the force required to be applied in the opposite direction, F = 2lT
Now, the amount of work done in displacing the wire AB through a short distance öx against the surface tension (assuming the force F to be a constant throughout the displacement) so that it comes to the new position A’B’ is
Fδx = 2lTδx
Due to this, the total increase in the area of the film surface = 2lδx.
This work remains stored as potential energy on the film surface.
Work done for unit increase in area against the surface tension = \(\frac{2 l T \delta x}{2 l \delta x}\) = T
So, the potential energy stored per unit area or the surface energy is numerically equal to the surface tension of the liquid. Note that the temperature is assumed to be constant.
Alternative definition of surface tension: Keeping the temperature constant, the amount of work done in increasing the area of a liquid surface by unity is called the surface tension of that liquid at that temperature.
Units:

Dimension:
According to the alternative definition,
[Surface tension] = \(\frac{\text { [work] }}{\text { [area] }}\) = \(\frac{\mathrm{ML}^2 \mathrm{~T}^{-2}}{\mathrm{~L}^2}\) = MT-2
Total surface energy: In the discussion, it was assumed that, during increase in the area of a liquid surface under the influence of an applied force, the temperature remains constant. But, in practice, some molecules from inside the liquid rise to its surface during the expansion of the surface. A resultant attraction exerted by the other molecules inside the liquid acts on these moving molecules.
Therefore, these molecules on reaching the surface lose their linear kinetic energy and the average linear kinetic energy of the total liquid decreases. Since the temperature is directly proportional to the average kinetic energy, the temperature of the surface of the liquid decreases with an increase in its area. To keep the temperature constant, the liquid surface absorbs heat from its surroundings. To increase the area of a liquid surface keeping the temperature constant, energy may be supplied in two ways-
- mechanical energy to increase the surface area and
- heat energy to keep the temperature constant. The total of these two energies should actually be the surface energy
So, the increase in potential energy per unit surface area or stored surface energy (E) = mechanical energy or work
done (T) + heat (h) required for unit area
i.e., E = T + h …………. (1)
From thermodynamics, it can be proved that,
h = -θ\(\frac{d T}{d \theta}\)
[θ = temperature in absolute scale and \(\frac{d T}{d \theta}\) rate of increase in surface tension due to increase in temperature]
∴ E = T – θ\(\frac{d T}{d \theta}\) …………. (2)
Now, with the increase in temperature, the surface tension decreases and hence \(\frac{d T}{d \theta}\) is a negative quantity.
So, h is a positive quantity.
∴ E = T + θ\(\frac{d T}{d \theta}\) ……….. (3)
when only the magnitudes are considered.
Again, at the absolute zero temperature, i.e., when θ = 0, E = T.
So, at any temperature except absolute zero, the total surface energy of a liquid is always greater than the surface tension of that liquid.
Factors Affecting Surface Tension of a Liquid
Surface tension of a liquid depends on the following factors.
1. Temperature of the Uquld: With an increase in the temperature, the surface tension of almost all liquids decreases. For a small change in temperature, the relation between surface tension and temperature is
T’ = T[1 – α(t’ – t)]
[Here, T and T’ are the surface tensions at temperatures t and t’ respectively]
For a given liquid, α is a constant quantity. It is called the temperature coefficient of surface tension.
It is experimentally verified that at a specific temperature of every liquid, the surface tension of the liquid disappears. This temperature is called the critical temperature of that liquid.
2. Pollution: If impurities are present on a liquid surface, then the surface tension of that liquid usually decreases. For example, when an oil or a fat-like substance is poured over water, it forms a thin film over the surface of water. This decreases the original surface tension of water.
3. Presence of dissolved substances: If a liquid contains dissolved inorganic substances, then the surface tension of that liquid increases. Again, if the liquid contains dissolved organic matter, then its surface tension decreases.
For example, the surface tension of pure water is 0.072 N ᐧ m-1. If common salt (inorganic substance) is dissolved in water, then its surface tension becomes 0.083 N ᐧ m-1 (approx.), but the surface tension of soap
water (organic substance) is approximately 0.030 N ᐧ m-1.
4. Medium above the liquid surface: The surface tension of a liquid depends on the nature of the medium above the free surface of that liquid. For example, the surface tension of water is about 72 dyn ᐧ cm-1 in the presence of dry air above the surface of water, but is about 70 dyn ᐧ cm-1 when there is moist air above the surface of water at the same temperature.
5. Presence of electric charge: The surface tension of a liquid decreases due to the presence of electric charge on the surface of the liquid.
Some Phenomena in Connection with Surface Tension
1. Camphor darts to and fro when put on the Surface of water: Camphor is soluble in water. When put on water, the portion that comes into contact with the water begins to dissolve. The part which gets dissolved in water contaminates the water and the surface tension of that part decreases. Due to this difference in surface tension, a net unbalanced force acts on the piece of camphor and consequently, the piece of camphor darts to and fro on the surface of water.
2. Hair of a paint brush cling together when the brush is brought out of water: The hair of a brush lie apart while immersed in water because, inside water, the surface tension is absent. ut when the brush is brought out of water, a thin film of water clings to the hair and the surface tension tries to contract the area of the film and hence the hair cling together.
3. Turbulent sea calms down if oil is poured on the water: The surface tension of pure water is more than that of oily water. When oil is poured over sea water, the oil spreads in the direction of motion of the waves leaving uncovered sea water at the rear. Hence, the surface tension of the water ahead of the waves is lower than that of the water behind the waves. The water at the rear pulls the water at the front and, as a result, high waves become lower.
4. When oil is poured on water it spreads, readily over the entire surface: Since the surface tension of pure water is greater than the surface tension of oil, a tensile force acts on the surface of oil. Due to this tensile force, oil spreads readily over the entire surface of water.
5. When chalk dust is sprinkled on water and a few drops of alcohol is added, then the dust particles rapidly spread on the water surface: Alcohol decreases the surface tension. Due to unequal surface tension on different parts of the water surface, the chalk particles spread rapidly on the surface of water.
6. Water cannot seep in through the cloth of raincoats umbrellas and tents: The minute pores in the cloth of raincoats etc. trap air molecules. However, these pores are too small to let rain droplets enter, because the droplets retain their spherical shape due to surface tension, and the diameters of the spheres are greater than that of the pores. So, the rainwater falling on the cloth simply flows off.
7. A needle cañ float on water surface: A needle floats due to the “s’urface tension of water. The surface of water where the needle is placed experiences a slight depression due to the surface tension of water. So, the water exerts an upward force on the needle which balances its weight (acting downwards) [Fig.]. Therefore, a needle can float if it is placed carefully on a calm water surface.

Surface Tension values of Various Liquids
| Liquid | Surface tension(N/m) | Liquid | Surface tension(N/m) |
| Ethyl Alcohol | 0.022 | Glycerine | 0.063 |
| Carbon Tetrachloride | 0.027 | Water | 0.072 |
| Soap Solution | 0.030 | Mercury | 0.465 |
Numerical Examples
Example 1.
The surface tension of water at 20°C is 72 dyn ᐧ cm-1 and for water \(\frac{d T}{d \theta}\) = -0.146 dyn ᐧ cm-1 ᐧ K-1. What is the total sur-face energy of water?
Solution:
We know that the total surface energy of water,
E = T – θ\(\frac{d T}{d \theta}\) = 72 – 293 × (-0.146) [20°C = 293 K]
= 72 + 42.778 = 114.778 erg ᐧ cm-2
Example 2.
A drop of water of radius 1 mm is to be divided into 106 point drops of equal size. How much mechanical work should be done? The surface tension of water = 72 dyn ᐧ cm-1.
Solution:
Let the radius of each point drop be r
∴ \(\frac{4}{3} \pi r^3\) × 106 = \(\frac{4}{3} \pi\left(\frac{1}{10}\right)^3\) or, r = 0.001 cm
The surface area of the original drop 4π\(\left(\frac{1}{10}\right)^2\) cm2 and the total surface area of 106 point drops
= 106 × 4π(0.001)2 = 4π cm2.
∴ Increase in surface area
= 4π – 4π\(\left(\frac{1}{10}\right)^2\) = 4π × 0.99 cm2
∴ Mechanical work done = increase in surface area × surface tension
= 72 × 4π × 0.99 = 895.73 erg.
Example 3.
1000 water droplets having a radius of 0.01 cm each coalesce to form a single big drop. What will be the decrease in energy? The surface tension of water = 72 dyn ᐧ cm-1.
Solution:
Let the radius of the single big drop be R.
∴ \(\frac{4}{3}\)πR3 = \(\frac{4}{3}\)π(0.01)3 × 1000 or, R = 0.1 cm
Surface area of the big drop = 4π(0. 1)2 cm2
Total surface area of 1000 droplets
= 4π(0.01)2 × 1000 cm2
= 4π(0.1 – 0.01) = 4π × 0.09 cm2
∴ Decrease in area
= 4π(0.01)2 × 1000 – 4π(0.1)2
= 4π(0.1 – 0.01) = 4π × 0.09 cm2
∴ Decrease in energy
= 4π × 0.09 × 72 = 81.43 erg.
Example 4.
A rectangular glass slab measures 0.1 m × 0.0154 m × 0.002 m and its weight in air is 80.36 × 10-3 N. The slab is immersed half in water keeping its length and thickness horizontal. What will be the apparent weight of the slab? The surface tension of water is 72 × 10-3 N ᐧ m-1.
Solution:
While it is immersed, the following forces act on the glass slab—
- weight of the slab acting downwards,
- upward buoyant force due to the weight of displaced water and
- downward force due to surface tension.
Now, weight of the slab = 80.36 × 10-3 N
Buoyant force = weight of displaced water
= 0.1 × \(\frac{0.0154}{2}\) × 0.002 × 1000 × 9.8
= 15.092 × 10-3N
Force due to surface tension
= 2 × (0.1 + 0.002) × 72 × 10-3N
= 14.6888 × 10-3N
∴ The apparent weight of the slab
= 80.36 × 10-3 – 15.092 × 10-3 + 14.688 × 10-3
= 79.956 × 10-3N.
Example 5.
The radius of a soap-bubble is increased from 1 cm to 3 cm. What amount of work is done for this? The surface tension of soap-water is 26 dyn ᐧ cm-1.
Solution:
Work done = increase in area × surface tension
=4π{(3)2 – (1)2} × 26 × 2
[∵ the soap-bubble has two surfaces]
= 5227.6 erg = 5.2276 × 10-4J.
Example 6.
Determine the surface energy ola liquid film formed on a ring of area 0.15 m2. The surface tension of the liquid = 5 N ᐧ m-1. [EAMCET 2000]
Solution:
Surface energy,
E = 2 × surface tension × area = 2 × 5 × 0.15 = 1.5 J.
Example 7.
Determine the surface energy of a soap-water film formed on a frame of area 10-3 m2. Surface tension of soap-water = 70 × 10-3 N ᐧ m-1. [HS(XI) ‘09]
Solution:
Surface energy,
= 2 × surface tension × area
= 2 × 70 × 10-3 × 10 = 14 × 10-5J.
Example 8.
What will be the work done to form a soap-bubble of radius 5 cm? The surface tension of soap-water = 70 dyn ᐧ cm-1 [HS(XI)’09]
Solution:
Work done = 2 × 4πr2 × T = 8πr2T
[r = radius of the soap-bubble and
T = surface tension of soap-water]
= 8 × \(\frac{22}{7}\) × (5)2 × 70 = 44000 erg
= 0.0044 J
Example 9.
If a large number of water droplets of diameter 2r cm each coalesce to form a large water drop of diameter 2R cm, then prove that the rise in temperature of water is \(\frac{3 T}{J}\)(\(\frac{1}{r}\) – \(\frac{1}{R}\)) Here, T is the surface tension of water and J is the mechanical equivalent of heat.
Solution:
If the number of small water droplets is n, then the dissipation of surface energy, W = (4πr2n – 4πR2)T.
We know that W = JH and H = heat absorbed = msθ
[where m = mass of the larger water drop, s = specific heat of water, θ = temperature increase]

Example 10.
Water is filled upto a height h in a beaker of radius R as shown in the Fig. The density of water is ρ, the surface tension of water is T and the atmospheric pressure is P0. Consider a vertical section ABCÐ of the water column through a diameter of the beaker. What is the force on water on one side of this section by water on the other side of this section?

Solution:
The force acted on the liquid of left side by the liquid of right side is equal to the resultant of the following two forces.
i) Force due to surface tension = 2RT (right side).
ii) Impulse due to the exerted pressure by the liquid of height h
= (P0 + \(\frac{\rho g h}{2}\)) × 2Rh [where \(\frac{\rho g h}{2}\) = average pressure on the plane ABCD]
= 2P0Rh + Rρgh2 (along left side)
∴ The resultant force on the plane ABCD
= 2P0Rh + Rρgh2 – 2RT