NCERT Solutions for Class 12 Maths Chapter 3 Matrices Ex 3.3 are part of NCERT Solutions for Class 12 Maths . Here we have given NCERT Solutions for Class 12 Maths Chapter 3 Matrices Ex 3.3.
| Board | CBSE |
| Textbook | NCERT |
| Class | Class 12 |
| Subject | Maths |
| Chapter | Chapter 3 |
| Chapter Name | Matrices |
| Exercise | Ex 3.3 |
| Number of Questions Solved | 12 |
| Category | NCERT Solutions |
NCERT Solutions for Class 12 Maths Chapter 3 Matrices Ex 3.3
Ex 3.3 Class 12 Maths Question 1.
Find the transpose of each of the following matrices:
(i) \(\left[ \begin{matrix} 5 \\ \frac { 1 }{ 2 } \\ -1 \end{matrix} \right] \)
(ii) \(\begin{bmatrix} 1 & -1 \\ 2 & 3 \end{bmatrix}\)
(iii) \(\left[ \begin{matrix} -1 & 5 & 6 \\ \sqrt { 3 } & 5 & 6 \\ 2 & 3 & -1 \end{matrix} \right] \)
Solution:
(i) let A = \(\left[ \begin{matrix} 5 \\ \frac { 1 }{ 2 } \\ -1 \end{matrix} \right] \)
∴ transpose of A = A’ = \(\left[ \begin{matrix} 5 & \frac { 1 }{ 2 } & -1 \end{matrix} \right] \)

Ex 3.3 Class 12 Maths Question 2.
If \(A=\left[ \begin{matrix} -1 & 2 & 3 \\ 5 & 7 & 9 \\ -2 & 1 & 1 \end{matrix} \right] ,B=\left[ \begin{matrix} -4 & 1 & -5 \\ 1 & 2 & 0 \\ 1 & 3 & 1 \end{matrix} \right] \)
then verify that:
(i) (A+B)’=A’+B’
(ii) (A-B)’=A’-B’
Solution:
\(A=\left[ \begin{matrix} -1 & 2 & 3 \\ 5 & 7 & 9 \\ -2 & 1 & 1 \end{matrix} \right] ,B=\left[ \begin{matrix} -4 & 1 & -5 \\ 1 & 2 & 0 \\ 1 & 3 & 1 \end{matrix} \right] \)


Ex 3.3 Class 12 Maths Question 3.
If \(A’=\left[ \begin{matrix} 3 & 4 \\ -1 & 2 \\ 0 & 1 \end{matrix} \right] ,B=\left[ \begin{matrix} -1 & 2 & 1 \\ 1 & 2 & 3 \end{matrix} \right] \)
then verify that:
(i) (A+B)’ = A’+B’
(ii) (A-B)’ = A’-B’
Solution:
\(A’=\left[ \begin{matrix} 3 & 4 \\ -1 & 2 \\ 0 & 1 \end{matrix} \right] ,B=\left[ \begin{matrix} -1 & 2 & 1 \\ 1 & 2 & 3 \end{matrix} \right] \)


Ex 3.3 Class 12 Maths Question 4.
If \(A’=\begin{bmatrix} -2 & 3 \\ 1 & 2 \end{bmatrix},B=\begin{bmatrix} -1 & 0 \\ 1 & 2 \end{bmatrix} \)
then find (A+2B)’
Solution:
\(A’=\begin{bmatrix} -2 & 3 \\ 1 & 2 \end{bmatrix},B=\begin{bmatrix} -1 & 0 \\ 1 & 2 \end{bmatrix} \)

Ex 3.3 Class 12 Maths Question 5.
For the matrices A and B, verify that (AB)’ = B’A’, where
\((i)\quad A=\left[ \begin{matrix} 1 \\ -4 \\ 3 \end{matrix} \right] ,B=\left[ \begin{matrix} -1 & 2 & 1 \end{matrix} \right] \)
\((ii)\quad A=\left[ \begin{matrix} 0 \\ 1 \\ 2 \end{matrix} \right] ,B=\left[ \begin{matrix} 1 & 5 & 7 \end{matrix} \right] \)
Solution:
\((i)\quad A=\left[ \begin{matrix} 1 \\ -4 \\ 3 \end{matrix} \right] \)
\(A’=\left[ \begin{matrix} 1 & -4 & 3 \end{matrix} \right] \)
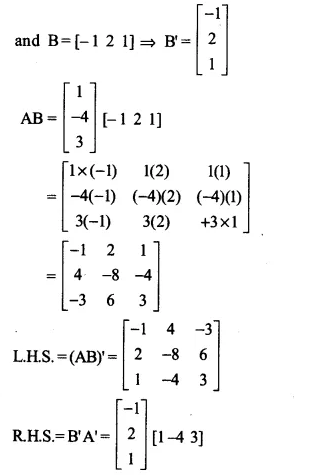
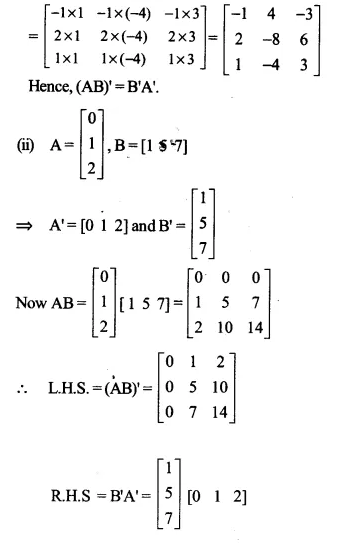

Ex 3.3 Class 12 Maths Question 6.
If (i) \(A=\begin{bmatrix} cos\alpha & \quad sin\alpha \\ -sin\alpha & \quad cos\alpha \end{bmatrix} \) ,the verify that A’A=I
If (ii) \(A=\begin{bmatrix} sin\alpha & \quad cos\alpha \\ -cos\alpha & \quad sin\alpha \end{bmatrix} \),the verify that A’A=I
Solution:
(i) \(A=\begin{bmatrix} sin\alpha & \quad cos\alpha \\ -sin\alpha & \quad cos\alpha \end{bmatrix} \)
\(A’=\begin{bmatrix} cos\alpha & \quad -sin\alpha \\ sin\alpha & \quad cos\alpha \end{bmatrix} \)

Ex 3.3 Class 12 Maths Question 7.
(i) Show that the matrix \(A=\left[ \begin{matrix} 1 & -1 & 5 \\ -1 & 2 & 1 \\ 5 & 1 & 3 \end{matrix} \right] \) is a symmetric matrix.
(ii) Show that the matrix \(A=\left[ \begin{matrix} 0 & 1 & -1 \\ -1 & 0 & 1 \\ 1 & -1 & 0 \end{matrix} \right] \) is a skew-symmetric matrix.
Solution:
(i) For a symmetric matrix aij = aji
Now,
\(A=\left[ \begin{matrix} 1 & -1 & 5 \\ -1 & 2 & 1 \\ 5 & 1 & 3 \end{matrix} \right] \)

Ex 3.3 Class 12 Maths Question 8.
For the matrix, \(A=\begin{bmatrix} 1 & 5 \\ 6 & 7 \end{bmatrix}\)
(i) (A+A’) is a symmetric matrix.
(ii) (A-A’) is a skew-symmetric matrix.
Solution:
\(A=\begin{bmatrix} 1 & 5 \\ 6 & 7 \end{bmatrix}\)
=> \(A’=\begin{bmatrix} 1 & 6 \\ 5 & 7 \end{bmatrix}\)

Ex 3.3 Class 12 Maths Question 9.
Find \(\\ \frac { 1 }{ 2 } (A+A’)\) and \(\\ \frac { 1 }{ 2 } (A-A’)\),when
\(A=\left[ \begin{matrix} 0 & a & b \\ -a & 0 & c \\ -b & -c & 0 \end{matrix} \right] \)
Solution:
\(A=\left[ \begin{matrix} 0 & a & b \\ -a & 0 & c \\ -b & -c & 0 \end{matrix} \right] \)
\(A’=\left[ \begin{matrix} 0 & -a & -b \\ a & 0 & -c \\ b & c & 0 \end{matrix} \right] \)

Ex 3.3 Class 12 Maths Question 10.
Express the following matrices as the sum of a symmetric and a skew-symmetric matrix.
(i)\(\begin{bmatrix} 3 & 5 \\ 1 & -1 \end{bmatrix}\)
(ii)\(\left[ \begin{matrix} 6 & -2 & 2 \\ -2 & 3 & -1 \\ 2 & -1 & 3 \end{matrix} \right] \)
(iii)\(\left[ \begin{matrix} 3 & 3 & -1 \\ -2 & -2 & 1 \\ -4 & -5 & 2 \end{matrix} \right] \)
(iv)\(\begin{bmatrix} 1 & 5 \\ -1 & 2 \end{bmatrix}\)
Solution:
(i) let \(A=\begin{bmatrix} 3 & 5 \\ 1 & -1 \end{bmatrix}\)
=> \(A’=\begin{bmatrix} 3 & 1 \\ 5 & -1 \end{bmatrix}\)

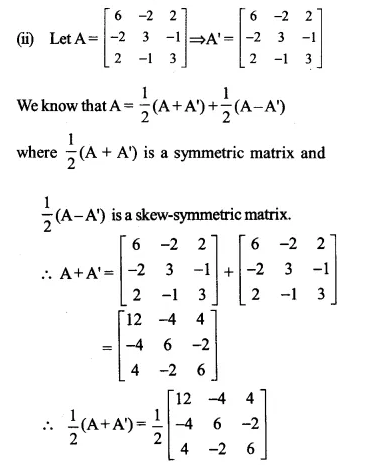




Ex 3.3 Class 12 Maths Question 11.
Choose the correct answer in the following questions:
If A, B are symmetric matrices of same order then AB-BA is a
(a) Skew – symmetric matrix
(b) Symmetric matrix
(c) Zero matrix
(d) Identity matrix
Solution:
Now A’ = B, B’ = B
(AB-BA)’ = (AB)’-(BA)’
= B’A’ – A’B’
= BA-AB
= – (AB – BA)
AB – BA is a skew-symmetric matrix Hence, option (a) is correct.
Ex 3.3 Class 12 Maths Question 12.
If \(A=\begin{bmatrix} cos\alpha & \quad -sin\alpha \\ sin\alpha & \quad cos\alpha \end{bmatrix}\) then A+A’ = I, if the
value of α is
(a) \(\frac { \pi }{ 6 } \)
(b) \(\frac { \pi }{ 3 } \)
(c) π
(d) \(\frac { 3\pi }{ 2 } \)
Solution:
Now

Thus option (b) is correct.
We hope the NCERT Solutions for Class 12 Maths Chapter 3 Matrices Ex 3.3 help you. If you have any query regarding NCERT Solutions for Class 12 Maths Chapter 3 Matrices Ex 3.3, drop a comment below and we will get back to you at the earliest.