NCERT Solutions for Class 12 Maths Chapter 7 Integrals Ex 7.5

NCERT Solutions for Class 12 Maths Chapter 7 Integrals Ex 7.5 are part of NCERT Solutions for Class 12 Maths. Here we have given NCERT Solutions for Class 12 Maths Chapter 7 Integrals Ex 7.5.

• Integrals Class 12 Ex 7.1
• Integrals Class 12 Ex 7.2
• Integrals Class 12 Ex 7.3
• Integrals Class 12 Ex 7.4
• Integrals Class 12 Ex 7.6
• Integrals Class 12 Ex 7.7
• Integrals Class 12 Ex 7.8
• Integrals Class 12 Ex 7.9
• Integrals Class 12 Ex 7.10
• Integrals Class 12 Ex 7.11

Board	CBSE
Textbook	NCERT
Class	Class 12
Subject	Maths
Chapter	Chapter 7
Chapter Name	Integrals
Exercise	Ex 7.5
Number of Questions Solved	23
Category	NCERT Solutions

NCERT Solutions for Class 12 Maths Chapter 7 Integrals Ex 7.5

Integrate the rational function in exercises 1 to 21

Ex 7.5 Class 12 Maths Question 1.
\(\frac { x }{ (x+1)(x+2) }\)
Solution:
let \(\frac { x }{ (x+1)(x+2) }\) ≡ \(\frac { A }{ x+1 } +\frac { B }{ x+2 } \)
⇒ x ≡ A(x+2)+B(x+1)….(i)
putting x = -1 & x = -2 in (i)
we get A = 1,B = 2
\(\therefore \int { \frac { 1 }{ (x+1)(x+2) } dx } =\int { \frac { -1 }{ x+1 } dx } +\int { \frac { 2 }{ x+2 } dx } \)
=-log|x+1| + 2log|x+2|+c

Ex 7.5 Class 12 Maths Question 2.
\(\frac { 1 }{ { x }^{ 2 }-9 } \)
Solution:
let \(\frac { 1 }{ { x }^{ 2 }-9 } =\frac { 1 }{ (x-3)(x+3) } \equiv \frac { A }{ x-3 } +\frac { B }{ x+3 } \)
⇒ x ≡ A(x+3)+B(x-3)…(i)
put x = 3, -3 in (i)
we get \(A=\frac { 1 }{ 6 }\) & \(B=-\frac { 1 }{ 6 }\)
\(\therefore \int { \frac { 1 }{ { x }^{ 2 }-9 } dx } =\frac { 1 }{ 6 } \int { \left[ \frac { 1 }{ x-3 } -\frac { 1 }{ x+3 } \right] dx } \)
\(=\frac { 1 }{ 6 } log\left| \frac { x-3 }{ x+3 } \right| +c\)

Ex 7.5 Class 12 Maths Question 3.
\(\frac { 3x-1 }{ (x-1)(x-2)(x-3) }\)
Solution:
Let \(\frac { 3x-1 }{ (x-1)(x-2)(x-3) } =\frac { A }{ x-1 } +\frac { B }{ x-2 } +\frac { C }{ x-3 } \)
⇒ 3x-1 = A(x-2)(x-3)+B(x-1)(x-3)+C(x-1)(-2)…..(i)
put x = 1,2,3 in (i)
we get A = 1,B = -5 & C = 4
\(\therefore I=\int { \frac { 1 }{ x-1 } dx } -5\int { \frac { 1 }{ x-2 } dx } +4\int { \frac { 1 }{ x-3 } dx } \)
=log|x-1| – 5log|x-2| + 4log|x+3| + C

Ex 7.5 Class 12 Maths Question 4.
\(\frac { x }{ (x-1)(x-2)(x-3) }\)
Solution:
let \(\frac { x }{ (x-1)(x-2)(x-3) } =\frac { A }{ x-1 } +\frac { B }{ x-2 } +\frac { C }{ x-3 } \)
⇒ x ≡ A(x-2)(x-3)+B(x-1)(x-3)+C(x-1)(x-2)…(i)
put x = 1,2,3 in (i)
\(A=\frac { 1 }{ 2 } ,B=-2,C=\frac { 3 }{ 2 } \)
\(\therefore I=\frac { 1 }{ 2 } \int { \frac { dx }{ x-1 } } -2\int { \frac { dx }{ x-2 } } +\frac { 3 }{ 2 } \int { \frac { dx }{ x-3 } } \)
\(=\frac { 1 }{ 2 } log|x-1|-2log|x-2|+\frac { 3 }{ 2 } log|x-3|+c \)

Ex 7.5 Class 12 Maths Question 5.
\(\frac { 2x }{ { x }^{ 2 }+3x+2 } \)
Solution:
let \(\frac { 2x }{ { x }^{ 2 }+3x+2 } =\frac { 2x }{ (x+1)(x+2) } =\frac { A }{ x+1 } +\frac { B }{ x+2 } \)
⇒ 2x = A(x+2)+B(x+1)…(i)
put x = -1, -2 in (i)
we get A = -2, B = 4
\(\therefore \int { \frac { 2x }{ { x }^{ 2 }+3x+2 } dx } =-2\int { \frac { dx }{ x+1 } } +4\int { \frac { dx }{ x+2 } } \)
=-2log|x+1|+4log|x+2|+c

Ex 7.5 Class 12 Maths Question 6.
\(\frac { 1-{ x }^{ 2 } }{ x(1-2x) } \)
Solution:
\(\frac { 1-{ x }^{ 2 } }{ (x-2{ x }^{ 2 }) } \) is an improper fraction therefore we
convert it into a proper fraction. Divide 1 – x² by x – 2x² by long division.

Ex 7.5 Class 12 Maths Question 7.
\(\frac { x }{ \left( { x }^{ 2 }+1 \right) \left( x-1 \right) } \)
Solution:
let \(\frac { x }{ \left( { x }^{ 2 }+1 \right) \left( x-1 \right) } =\frac { A }{ x-1 } +\frac { Bx+C }{ { x }^{ 2 }+1 } \)
⇒ x = A(x²+1)+(Bx+C)(x-1)
Put x = 1,0
⇒ \(A=\frac { 1 }{ 2 } C=\frac { 1 }{ 2 } \Rightarrow B=-\frac { 1 }{ 2 } \)
\(\therefore I=\frac { 1 }{ 2 } \int { \frac { dx }{ x-1 } } -\frac { 1 }{ 2 } \int { \frac { x }{ { x }^{ 2 }+1 } dx } +\frac { 1 }{ 2 } \int { \frac { dx }{ { x }^{ 2 }+1 } } \)
\(=\frac { 1 }{ 2 } log(x-1)-\frac { 1 }{ 4 } log({ x }^{ 2 }+1)+\frac { 1 }{ 2 } { tan }^{ -1 }x+c \)

Ex 7.5 Class 12 Maths Question 8.
\(\frac { x }{ { \left( x-1 \right) }^{ 2 }\left( x+2 \right) } \)
Solution:
\(\frac { x }{ { \left( x-1 \right) }^{ 2 }\left( x+2 \right) } =\frac { A }{ x-1 } +\frac { B }{ { \left( x-1 \right) }^{ 2 } } +\frac { C }{ x+2 } \)
⇒ x ≡ A(x-1)(x+2)+B(x+2)+C(x-1)² …(i)
put x = 1, -2
we get \(B=\frac { 1 }{ 3 } ,C=\frac { -2 }{ 9 } \)
\(\therefore I=\frac { 2 }{ 9 } \int { \frac { 1 }{ x-1 } dx } +\frac { 1 }{ 3 } \int { \frac { 1 }{ { (x-1) }^{ 2 } } dx } -\frac { 2 }{ 9 } \int { \frac { 1 }{ x+2 } dx } \)
\(=\frac { 2 }{ 9 } log\left| \frac { x-1 }{ x+2 } \right| -\frac { 1 }{ 3\left( x-1 \right) } +c\)

Ex 7.5 Class 12 Maths Question 9.
\(\frac { 3x+5 }{ { x }^{ 3 }-{ x }^{ 2 }-x+1 } \)
Solution:
let \(\frac { 3x+5 }{ { x }^{ 2 }(x-1)-1(x-1) } \)
\(\frac { 3x+5 }{ (x-1)^{ 2 }(x+1) } =\frac { A }{ x-1 } +\frac { B }{ { (x-1) }^{ 2 } } +\frac { C }{ x+1 } \)
⇒ 3x+5 = A(x-1)(x+1)+B(x+1)+C(x-1)
put x = 1,-1,0
we get \(B=4,C=\frac { 1 }{ 2 } ,A=-\frac { 1 }{ 2 } \)
\(\therefore I=-\frac { 1 }{ 2 } \int { \frac { dx }{ (x-1) } } +4\frac { dx }{ { (x-1) }^{ 2 } } +\frac { 1 }{ 2 } \int { \frac { dx }{ x+1 } } \)
\(=\frac { 1 }{ 2 } log\left| \frac { x+1 }{ x-1 } \right| -\frac { 4 }{ x-1 } +c\)

Ex 7.5 Class 12 Maths Question 10.
\(\frac { 2x-3 }{ ({ x }^{ 2 }-1)(2x+3) } \)
Solution:
\(\frac { 2x-3 }{ ({ x }^{ 2 }-1)(2x+3) } =\frac { 2x-3 }{ (x-1)(x+1)(2x+3) } \)

Ex 7.5 Class 12 Maths Question 11.
\(\frac { 5x }{ (x-1)({ x }^{ 2 }-4) } \)
Solution:
let \(\frac { 5x }{ (x-1)({ x }^{ 2 }-4) } =\frac { 5x }{ (x+1)(x+2)(x-2) } \)

Ex 7.5 Class 12 Maths Question 12.
\(\frac { { x }^{ 3 }+x+1 }{ { x }^{ 2 }-1 } \)
Solution:
\(\frac { { x }^{ 3 }+x+1 }{ { x }^{ 2 }-1 } =x+\frac { 2x+1 }{ (x+1)(x-1) } \)

Ex 7.5 Class 12 Maths Question 13.
\(\frac { 2 }{ (1-x)(1+{ x }^{ 2 }) } \)
Solution:
\(\frac { 2 }{ (1-x)(1+{ x }^{ 2 }) } =\frac { A }{ 1-x } +\frac { Bx+C }{ 1+{ x }^{ 2 } } \)
⇒ 2 = A(1+x²) + (Bx+C)(1 -x) …(i)
Putting x = 1 in (i), we get; A = 1
Also 0 = A – B and 2 = A + C ⇒B = A = 1 & C = 1

Ex 7.5 Class 12 Maths Question 14.
\(\frac { 3x-1 }{ { (x+2) }^{ 2 } } \)
Solution:
\(\frac { 3x-1 }{ { (x+2) }^{ 2 } } \equiv \frac { A }{ x+1 } +\frac { B }{ { (x+2) }^{ 2 } } \)
=>3x – 1 = A(x + 2) + B …(i)
Comparing coefficients A = -1 and B = -7
\(\therefore \int { \frac { 3x-1 }{ { (x+2) }^{ 2 } } dx } =3\int { \frac { dx }{ x+2 } } -7\int { \frac { dx }{ { (x+2) }^{ 2 } } } \)
\(=3log|x+2|+\frac { 7 }{ x+2 } +c\)

Ex 7.5 Class 12 Maths Question 15.
\(\frac { 1 }{ { x }^{ 4 }-1 } \)
Solution:
\(\frac { 1 }{ { x }^{ 4 }-1 } =\frac { A }{ x+1 } +\frac { B }{ x-1 } +\frac { Cx+D }{ { x }^{ 2 }+1 } \)
⇒ 1 ≡ A(x-1)(x²+1) + B(x+1)(x²+1) + (Cx+D)(x+1)(x-1) ….(i)

Ex 7.5 Class 12 Maths Question 16.
\(\frac { 1 }{ x({ x }^{ n }+1) } \)
[Hint : multiply numerator and denominator by x^n-1 and put xⁿ = t ]
Solution:
\(\frac { { x }^{ n-1 } }{ x.{ x }^{ n-1 }({ x }^{ n }+1) } =\frac { { x }^{ n-1 } }{ { x }^{ n }({ x }^{ n }+1) } \)

Ex 7.5 Class 12 Maths Question 17.
\(\frac { cosx }{ (1-sinx)(2-sinx) } \)
Solution:
put sinx = t
so that cosx dx = dt
\(\therefore I=\int { \frac { 1 }{ (1-t)(2-t) } dt } \)

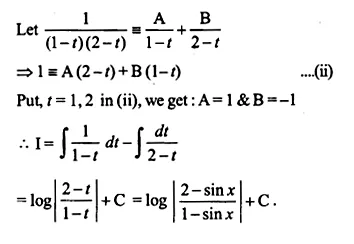
Ex 7.5 Class 12 Maths Question 18.
\(\frac { \left( { x }^{ 2 }+1 \right) \left( { x }^{ 2 }+2 \right) }{ \left( { x }^{ 2 }+3 \right) \left( { x }^{ 2 }+4 \right) } \)
Solution:
put x²=y
\(I=1-\frac { 2(2y+5) }{ (y+3)(y+4) } \)

Ex 7.5 Class 12 Maths Question 19.
\(\frac { 2x }{ ({ x }^{ 2 }+1)({ x }^{ 2 }+3) } \)
Solution:
put x²=y
so that 2xdx = dy
\(\therefore \int { \frac { 2x }{ ({ x }^{ 2 }+1)({ x }^{ 2 }+3) } dx } =\int { \frac { dy }{ (y+1)(y+3) } } \)

Ex 7.5 Class 12 Maths Question 20.
\(\frac { 1 }{ x({ x }^{ 4 }-1) } \)
Solution:
put x⁴ = t
so that 4x³ dx = dt

Ex 7.5 Class 12 Maths Question 21.
\(\frac { 1 }{ { e }^{ x }-1 } \)
Solution:
Let e^x = t ⇒ e^x dx = dt
⇒ \(dx=\frac { dt }{ t }\)

Ex 7.5 Class 12 Maths Question 22.
choose the correct answer in each of the following :
\(\int { \frac { xdx }{ (x-1)(x-2) } equals } \)
(a) \(log\left| \frac { { (x-1) }^{ 2 } }{ x-2 } \right| +c\)
(b) \(log\left| \frac { { (x-2) }^{ 2 } }{ x-1 } \right| +c\)
(c) \(log\left| \left( \frac { x-{ 1 }^{ 2 } }{ x-2 } \right) \right| +c\)
(d) log|(x-1)(x-2)|+c
Solution:
(b) \(\int { \frac { x }{ (x-1)(x-2) } dx } =\int { \left[ \frac { -1 }{ x-1 } +\frac { 2 }{ x-2 } \right] dx } \)
\(log\left| \frac { { (x-2) }^{ 2 } }{ x-1 } \right| +c\)

Ex 7.5 Class 12 Maths Question 23.
\(\int { \frac { dx }{ x({ x }^{ 2 }+1) } equals } \)
(a) \(log|x|-\frac { 1 }{ 2 } log({ x }^{ 2 }+1)+c \)
(b) \(log|x|+\frac { 1 }{ 2 } log({ x }^{ 2 }+1)+c \)
(c) \(-log|x|+\frac { 1 }{ 2 } log({ x }^{ 2 }+1)+c\)
(d) \(\frac { 1 }{ 2 } log|x|+log({ x }^{ 2 }+1)+c \)
Solution:
(a) let \(\frac { 1 }{ x\left( { x }^{ 2 }+1 \right) } =\frac { A }{ x } +\frac { Bx+C }{ { x }^{ 2 }+1 } \)
⇒ 1 = A(x²+1)+(Bx+C)(x)

We hope the NCERT Solutions for Class 12 Maths Chapter 7 Integrals Ex 7.5 help you. If you have any query regarding NCERT Solutions for Class 12 Maths Chapter 7 Integrals Ex 7.5, drop a comment below and we will get back to you at the earliest.