Fractions: Adding Fractions When the Denominators are the Same

In order to add two or more like fractions, we may follow the following steps:

Step 1) Obtain the fractions.
Step 2) Add the numerators of all fractions.
Step 3) Retain the common denominator of all fractions.
Step 4) Write fraction as \(\frac{Result in Step (2)}{Result in Step (3)}\)

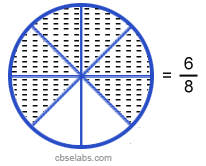
Adding Fractions When the Denominators are the Same Example 1:

Add the following fractions with the help of a diagram.

Solution: Given fractions are \(\frac{2}{8}, \frac{3}{8} and \frac{1}{8} respectively. Their addition is given by:\)

Adding Fractions When the Denominators are the Same Example 2:

Add the following fractions: 1) \(\frac{1}{6} + \frac{4}{6}\)

2) \(\frac{2}{7} + \frac{3}{7} + \frac{4}{7}\)
Solution: 1) We have,

\(\frac{1}{6} + \frac{4}{6}\) = \(\frac{1 + 4}{6}\) = \(\frac{5}{6}\)

2) We have,

\(\frac{2}{7} + \frac{3}{7} + \frac{4}{7}\) = \(\frac{2 + 3 + 4}{7}\) = \(\frac{9}{7}\)

Adding Fractions When the Denominators are the Same Example 3:

Add the following fractions: 1) \(2\frac{3}{5}\) + \(\frac{4}{5}\) + \(1\frac{2}{5}\)

2) \(1\frac{1}{4}\) + \(2\frac{3}{4}\) + \(7\frac{1}{4}\)

Solution: 1) We have,

\(2\frac{3}{5}\) + \(\frac{4}{5}\) + \(1\frac{2}{5}\) = \(\frac{10 +3}{5}\) + \(\frac{4}{5}\) + \(\frac{5 +2}{5}\)

= \(\frac{13}{5}\) + \(\frac{4}{5}\) + \(\frac{7}{5}\)

= \(\frac{13 + 4 + 7}{5}\) = \(\frac{24}{5}\)

2) We have,

\(1\frac{1}{4}\) + \(2\frac{3}{4}\) + \(7\frac{1}{4}\) = \(\frac{4 + 1}{4}\) + \(\frac{8 + 3}{4}\) + \(\frac{28 + 1}{4}\)

= \(\frac{5}{4}\) + \(\frac{11}{4}\) + \(\frac{29}{4}\)

= \(\frac{5 + 11 + 29}{4}\) = \(\frac{45}{4}\)

Adding Fractions When the Denominators are the Same Example 4:

Add \(\frac{2}{13}\) and \(\frac{7}{13}\).

Solution: \(\frac{2}{13}\) and \(\frac{7}{13}\) are like fractions.

In order to add them, just add the numerators without changing the denominator.

i.e., \(\frac{2}{13} + \frac{7}{13}\) = \(\frac{2 + 7}{13}\)

= \(\frac{9}{13}\)

Thus, \(\frac{2}{13} + \frac{7}{13}\) = \(\frac{9}{13}\).

Adding Fractions When the Denominators are the Same Example 5:

Add \(\frac{1}{12}\), \(\frac{3}{12}\) and \(\frac{5}{12}\).

Solution: \(\frac{1}{12}\), \(\frac{3}{12}\) and \(\frac{5}{12}\) are like fractions.

In order to add them, just add the numerators without changing the denominator.

i.e., \(\frac{1}{12} + \frac{3}{12} + \frac{5}{12}\) = \(\frac{1 + 3 + 5}{12}\)

= \(\frac{9}{12}\)

Thus, \(\frac{1}{12} + \frac{3}{12} + \frac{5}{12}\) = \(\frac{9}{12}\).