NEET Physics Chapter Wise Mock Test – Oscillations

NEET Physics Chapter Wise Mock Test – Oscillations

Question 1:
An elastic ball is dropped from a certain height and returns to the same height after elastic collision on the floor. What is the nature of repeated motion of the ball?
(a) Simple harmonic, oscillatory and periodic
(b) Simple harmonic, oscillatory but not periodic
(c) Simple harmonic, periodic, but not oscillatory
(d) Oscillatory, periodic but not simple harmonic

Question 2:
The graph between restoring force and time in case of SHM is
(a) a straight line
(b) a circle
(c) a parabola
(d) a sine curve

Question 3:
The displacement of SHM is given by
y = 5 cos(10t + 0.6)
What is the initial phase of the SHM?
(a) 5 rad
(b) 10 rad
(c) 0.6 rad
(d) None of these

Question 4:
A system is subjected to two SHMs given by
y₁ = 6 cosωt and y₂ = 8 cosωt The resultant amplitude of SHM is given by
(a) 2
(b) 10
(c) 14
(d) 20

Question 5:
A mass of 2.0 kg is put on a flat pan attached to a vertical spring fixed on the ground as shown in the figure. The mass of the spring and the pan is negligible. When pressed slightly and released the mass executes a simple harmonic motion. The spring constant is 200 Nm^-1. What should , be the minimum amplitude of the motion, so that the mass gets detached from the pan? (take, g = 10 ms^-2)

(a) 8.0 cm
(b) 10.0 cm
(c) Any value less than 12.0 cm
(d) 4.0 cm

Question 6:
The displacement of a particle varies with time according to the relation y = a sinωt + b cosωt
(a) The motipn is oscillatory but not SHM
(b) The motion is SHM with amplitude a + b
(c) The motion is SHM with amplitude a² + b²
(d) The motion is SHM with amplitude √(a² + b²)

Question 7:
A particle executes simple harmonic oscillation with an amplitude a. The period of oscillation is T. The minimum time taken by the particle to travel half of the amplitude from the equilibrium position is
(a) T/4
(b) T/8
(c) T/12
(6) T/2

Question 8:
A particle executes SHM with a period of T second and amplitude A metre. The shortest time it takes to reach point metre from its mean position in seconds is
(a) T
(b) T/4
(c) T/8
(6) T/16

Question 9:
Figure shows the circular motion of a particle. The radius of the circle, the period, sense of revolution and the initial position are indicated on the figure. The simple harmonic motion of the x-projection of the radius vector of the rotating particle P is

Question 10:
The equations of two linear SHM’s are x=a sinωt, along X-axis y = a sin2ωt, along Y-axis If they act on a particle simultaneously, the trajectory of the particle is

Question 11:
The time period of a SHM is 16 s. It starts its motion from the equilibrium position. After 2 s its velocity is Π ms^-1. What is its displacement amplitude?
(a) √2 m
(b) 2√2 m
(c) 4√2 m
(d) 8√2 m

Question 12:
If at any time the displacement of a simple pendulum be 0.02 m, then its acceleration is 2 ms^-2. What is the angular speed of the pendulum at that instant?
(a) 100 rads^-1
(b) 10 rads^-1
(c) 1 rads^-1
(d) 0.1 rads^-1

Question 13:
The x-t graph of a particle undergoing simple harmonic motion is shown below. The acceleration of the particle at t= 4 / 3 s is

Question 14:
If the length of a pendulum is quadrupled, its time period is
(a) quadrupled
(b) halved
(c) doubled
(d) unchanged

Question 15:
A SHM has an amplitude A and time period T. The time required by it to travel from x = A to x =A/2 is
(a) T/6
(b) T/4
(c) T/3
(d) T/2

Question 16:
A tunnel is bored along the diameter of the earth and a stone is dropped into it. What happens to the stone?
(a) It oscillates between the two ends of the tunnel
(b) It comes to rest at the centre of the earth
(c) It will go out of the other end of the tunnel
(d) It will come to a permanent stop at the other end of the tunnel

Question 17:
A tunnel is made along a chord inside the earth and a ball is released in it. What will be the time period of oscillation of the ball?
(a) 2Π √(R/2g)
(b) 2Π √(R/g)
(c) 2Π √(2R/g)
(d) Π √(R/g)

Question 18:
The displacement of a particle is represented by the equation y = 3 cos (Π/4-2ωt). The motion of the particle is
(a) simple harmonic with period 2Π/ω
(b) simple harmonic with period Π/ω
(c) periodic but not simple harmonic
(d) non-periodic

Question 19:
A particle moves such that its acceleration, a is given by a = -bx, where x is the displacement from equilibrium position and b is a constant. The period of oscillation is
(a) 2Π √b
(b) 2Π/√b
(c) 2Π/b
(d) 2√( pi/b)

Question 20:
A cylindrical piston of mass M slides smoothly inside a long cylinder closed at one end, enclosing a certain mass of gas. The cylinder is kept with its axis horizontal. If the piston is disturbed from its equilibrium position, it oscillates simple harmonically. Its period is

Question 21:
A spring is vibrating with frequency n under some mass. If it is cut into two equal parts and same mass is suspended, then the new frequency is
(a) n/2
(b) n
(c) n √2
(d) n/√2

Question 22:
From the ceiling of a train, a pendulum of length l is suspended. The train is moving with an acceleration a0 on horizontal surface. The period of oscillation of the pendulum is

Question 23:
A wire of length l, area of cross-section A and Young’s modulus of elasticity Y is suspended from the roof of a building. A block of mass m is attached at lower end of the wire. If the block is displaced from its mean position and released, then the block starts oscillating. Time period of these oscillations will be

Question 24:
A block of mass m is suspended by different springs of force constant shown in figure.

Let time period of oscillation in these four positions be T1, T2, T3 and T4. Then, which of the following statement is correct?
(a) T₁=T₂=T₄
(b) T₁ = T₂ and T₃ = T₄
(c) T₁=T₂=T₃
(d) T₁= T₃ and T₂ = T₄

Question 25:
On a smooth inclined plane a body of mass M is attached between two springs. The other ends of the springs are fixed to firm supports. If each spring has a force constant’ k, the period of oscillation of the body is (assuming the spring as massless)

Question 26:
A rectangular block of mass m and area of cross-section A floats in a liquid of density ρ. If it is given a small vertical displacement from equilibrium it undergoes oscillation with a time period T. Then,
(a) T ∝ √ρ
(b) T ∝ 1/√A
(c) T ∝ 1/√ρ
(d) T ∝ 1/√m

Question 27:
A girl is sitting on the roof of a flat toy car of mass 6 kg. If no slipping takes place between car and the girl, then what should be the mass of the child in order to have period of system equal to 0.758 s?

(a) 9 kg
(b) 2.74kg
(c) 6kg
(d) 7.28

Question 28:
In the given figure, the spring has a force constant k. The pulley is light and smooth the spring and string are light. The suspended block has a mass m. If the block is slightly displaced from its equilibrium position and then released. The period of its vertical oscillation is

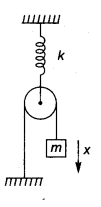
(a) 2π √(m/k)
(b) 4π√(m/k)
(c) 2π √(k/m)
(d) 4π √(k/m)

Question 29:
Two springs of force constants k₁, and k₂ are connected in series. The spring constant of the combination is
(a) k₁+k₂
(b) (k₁+k₂)/2
(c) (k₁+k₂)/k₁k₂
(d) k₁k₂/(k₁+k₂)

Question 30:
What will be the force constant of the spring system as shown in the figure?

Question 31:
As shown in figure, a simple harmonic motion oscillator having identical four springs has time period.

Question 32:
The mass M shown in the figure oscillates in simple harmonic motion with amplitude A. The amplitude of the point P is

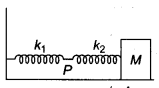
(a) k₁A/k₂
(b) k₂A/k₁
(c) k₁A/(k₁+k₂)
(d) k₂A/(k₁+k₂)

Question 33:
The particle executing SHM has a kinetic energy K₀cos²ωt. The maximum values of the potential energy and the total energy respectively are
(a) 0 and 2K₀
(b) K₀/2 and K₀
(c) K₀ and 2K₀
(d) K₀ and K₀

Question 34:
A load of mass m falls from a height h on to the scale pan hung from a spring as shown in figure. If the spring constant is k and mass of the scale pan is zero and the mass m does not bounce relative to the pan, then the amplitude of vibration is

Question 35:
The angular frequency and amplitude of a simple pendulum are ω and A, respectively. At the displacement y from the mean position, the kinetic energy is K and potential energy is U. What is the ratio of K/U ?
(a) MA²ω²sin²ωt
(b) MA²ω²cos²ωt
(c) (A²-y²)/y²
(d) y²/(A²-y²)

Question 36:
The potential energy of a long spring when stretched by 2 cm is U. If the spring is stretched by 8 cm, the potential energy stored in it is
(a) 4U
(b) 8U
(c) 16 U
(d) U/4

Question 37:
A particle executing simple harmonic motion of amplitude 5 cm has maximum speed of 31.4 cms^-1. The frequency of its oscillation is
(a) 3 Hz
(b) 2 Hz
(c) 4 Hz
(d) 1 Hz

Question 38:
The total energy of SHM is E. What will be the kinetic energy of the particle, when displacement is half of the amplitude?
(a) √3 E/2
(b) E/2
(c) 3E/4
(d) E/3

Question 39:
A body executing SHM has amplitude of 4 cm. What is the distance at which the body has equal value of both KE and PE?
(a) 2√2 cm
(b) 1/√2 cm
(c) √2 cm
(d) √2/6 cm

Question 40:
A mass of 0.5 kg moving with a speed of 1.5 ms^-1 on a horizontal smooth surface, collides with a nearly weightless ‘ spring of force constant k = 50Nm^-1. compression of the spring would be

(a) 0.15 m
(b) 0.12 m
(c) 1.5m
(d) 0.5m

Question 41:
The amplitude of a damped oscillator becomes half in 1 min. The amplitude after 3 min will be 1/X times the original, where X is
(a) 2×3
(b) 2³
(c) 3²
(d) 3 x 2²

Question 42:

Direction (Q. Nos. 43-45): In each of the following questions a statement of Assertion is given followed by a corresponding statement of Reason just below it. Of the statements mark the correct answer as
(a) If both Assertion and Reason are true and the Reason is the correct explanation of the Assertion
(b) If both Assertion and Reason are true but the Reason is not the correct explanation of the Assertion
(c) If Assertion is true but Reason is false
(d) If both Assertion and Reason are false

Question 43:
Assertion (A): The time period of a simple pendulum of infinite length is finite.
Reason (R): The time period of simple pendulum is directly proportional to the square root of length.

Question 44:
Assertion (A): The bob of a simple pendulum is a ball full of water. If a fine hole is made at the bottom of the ball, then the time period will no more remain constant.
Reason (R): The time period of a simple pendulum does not deperfd upon mass.

Question 45:
Assertion (A): A spring of force constant k is cut into two pieces whose lengths are in the ratio 1:2. The force constant of series combination of the two parts is 3k/2.
Reason (R): The spring connected in series are represented by k = k₁ + k₂.

Question 46:
When two displacements represented by y₁ = a sin (ωt) and y₂=b cos (ωt) are superimposed the motion is
(a) not a simple harmonic
(b) simple harmonic with amplitude a/b
(c) simple harmonic with amplitude √(a²+b²)
(d) simple harmonic with amplitude (a+b)/2

Question 47:
A particle is executing SHM along a straight line. Its velocities at distances x₁ and x₂ from the mean position are v₁ and v₂, respectively. Its time period is

Question 48:
Assertion (A): The periodic time of hard spring is less as compared to that of a soft string.
Reason (R): The periodic time depends upon the spring constant.

(a) If both assertion and reason are true and reason is the correct explanation of assertion
(b) If both assertion and reason ar’e true but the reason is not the correct explanation of assertion
(c) If assertion is true but reason is false
(d) If both assertion and reason are false

Question 49:
A simple harmonic oscillator consists of a particle of mass m and an ideal spring with spring constant k. The particle oscillates with a time period T. The spring is cut into two equal parts. If one part oscillates .with the same particle, the time period will be
(a) 2T
(b) √2 T
(c) T/√2
(d) T/2

Question 50:
When a string is divided into three segments of lengths l₁, l₂ and l₃, the fundamental frequencies of these three segments are ν₁, ν₂ and ν₃, respectively. The original fundamental frequency (ν) of the string is

Question 51:
A simple pendulum with length L and mass of the bob is vibrating with an amplitude a. Then, the maximum tension in the string is

Question 52:
Two simple pendulums first of bob mass M₁ and length L₁ second of bob mass M₂ and length L₂ . M₁ = M₂ and L₁ = 2L₂. If the vibrational energies of both are same. Then, which is correct?
(a) Amplitude of B greater than A
(b) Amplitude of B smaller than A
(c) Amplitude will be same
(d) None of the above

Question 53:
One-fourth length of a spring of force constant k is cut away. The force constant of the remaining spring will be
(a) 3k/4
(b) 4k/3
(c) k
(d) 4k

Question 54:
The displacement of a particle along the X-axis is given by x = asin²ωt. The motion of the particle corresponds to
(a) simple harmonic motion of frequency ω/π
(b) simple harmonic motion of frequency 3ω/π
(c) non-simple harmonic motion
(d) simple harmonic motion of frequency ω/2π

Question 55:
The period of oscillation of a mass M suspended from a spring of negligible mass is T. If along with it another mass M is also suspended, the period of oscillation will now be
(a) T
(b) T/√2
(c) 2T
(d) √2T

Answers:

Hints And Solutions:

PhysicsChemistryBiology